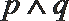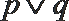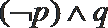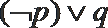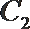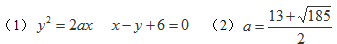- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. “


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 下列函数中,图象不关于原点对称的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 定积分
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 命题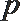
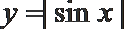
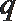
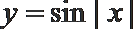
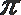
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 若曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 在△




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 关于函数
①最小正周期为
②图象关于
③图象关于点
④在区间
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
13. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知△


正确答案
直角三角形
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列



(1)证明数列
(2)求数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知△





(1)求∠B的大小。
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某射手击中目标的概率为0.8,现给他五发子弹,规定只要击中目标立即停止射击;没击中目标,继续射击,直到子弹全部打完为止。
(1)求射手射击三次的概率。
(2)若用


正确答案
(1)0.032 (2)3.7504
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆



(1)若椭圆、双曲线、抛物线在第一象限交于同一点
(2)若双曲线与抛物线在第一象限交于




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 在直角坐标系中,以原点为极点,以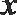

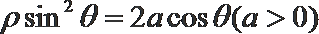
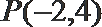
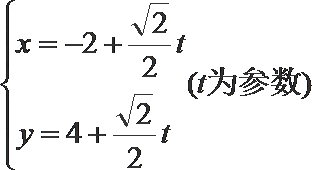
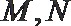
(1)求曲线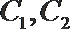
(2)若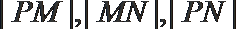
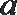
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数


(1)求函数
(2)证明:


正确答案
解析
解析已在路上飞奔,马上就到!