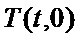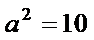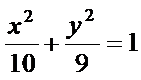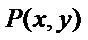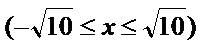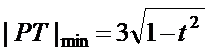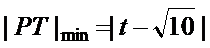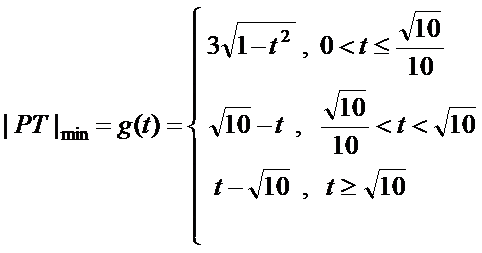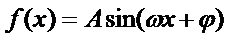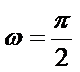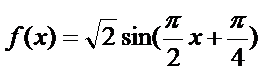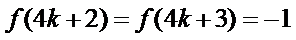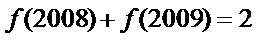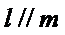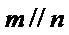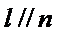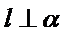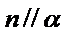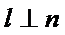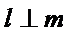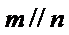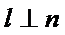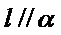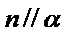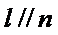- 真题试卷
- 模拟试卷
- 预测试卷
1.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知平面向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.

正确答案
45
解析
解析已在路上飞奔,马上就到!
知识点
5.计算: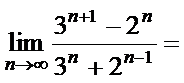
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在某地奥运火炬传递活动中,有编号为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数
①
②
③
④
其中对于



正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
14.如果











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.关于

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.无穷数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.一个长方体的各个顶点均在同一球面上,且一个顶点上的三条棱长分别为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线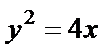
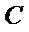
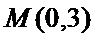
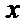
(1)求椭圆的标准方程
(2)设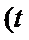
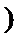
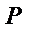
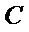
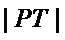

正确答案
(1)焦点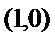
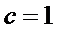
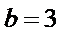
∴ 椭圆的方程为
(2)设
∴
当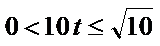
当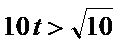
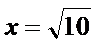
∴
解析
解析已在路上飞奔,马上就到!
知识点
23.若数列




(1)写出一个E数列

(2)若


(3)在


正确答案
解:(1)0,1,0,1,0是一具满足条件的E数列A5.
(答案不唯一,0,—1,0,1,0;0,±1,0,1,2;0,±1,0,—1,—2;0,±1,0,—1,
—2,0,±1,0,—1,0都是满足条件的E的数列A5)
(2)必要性:因为E数列A5是递增数列,
所以
所以A5是首项为12,公差为1的等差数列.
所以a2000=12+(2000—1)×1=2011.
充分性,由于a2000—a1000≤1,
a2000—a1000≤1
……
a2—a1≤1
所以a2000—at≤19999,即a2000≤a1+1999.
又因为a1=12,a2000=2011,
所以a2000=a1+1999.
故
综上,结论得证.
(3)对首项为4的E数列Ak,由于
……
……
所以
所以对任意的首项为4的E数列Am,若
则必有
又
所以n是最小值是9.
解析
解析已在路上飞奔,马上就到!
知识点
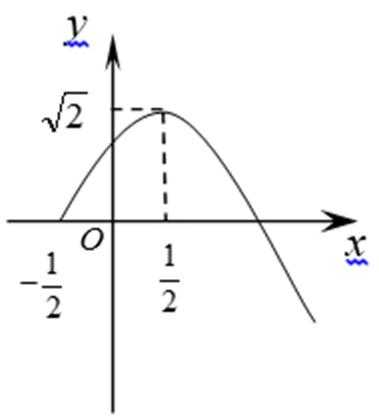
19.若函数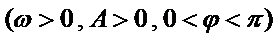
(1)求出函数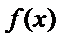
(2)求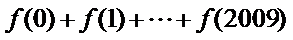
正确答案
(1)由图知:
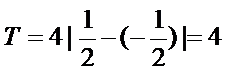
∴ 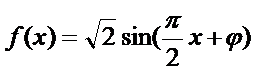
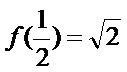
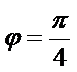
∴
(2)由(1)得 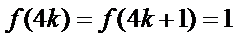
∴ 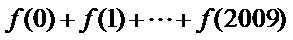
解析
解析已在路上飞奔,马上就到!
知识点
20.设二次函数



(1)求函数
(2)若对于任意的


正确答案
(1)设
∵ 

∴
∴
(2)
∴
即
解析
解析已在路上飞奔,马上就到!
知识点
22.对于函数








(1)判断函数
(2)已知







(3)在(2)的条件下,试比较

正确答案
(1)
∴
∴ 是“幅度函数”,其“幅度”为2
(2)
∵ 


∴ 当
当
∴ 
∴
(3)
令

∴
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
15.已知直线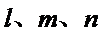
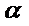
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如下图,根据该流程图,可以得出该算法的功能是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在数列



①在差等比数列中

②等差数列一定是差等比数列
③等比数列一定是差等比数列
④差等比数列中可以有无数项为
其中正确的判断是( )
正确答案
解析
解析已在路上飞奔,马上就到!