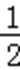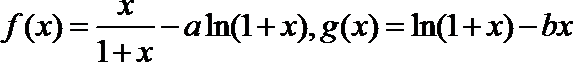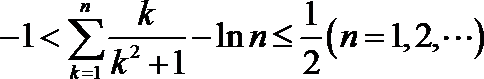- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合A={x|1<x<4},集合B={x|x2-2x-3≤0},则A∩(∁RB)=( )
正确答案
解析
由题意B={x|x2﹣2x﹣3≤0}={x|﹣1≤x≤3},故∁RB={x|x<﹣1或x>3},又集合A={x|1<x<4},∴A∩(∁RB)=(3,4),故选B
知识点
7. 已知点A(-1,1)、B(1,2)、C(-2,-1)、D(3,4),则向量
正确答案
解析
因为点A(﹣1,1)、B(1,2)、C(﹣2,﹣1)、D(3,4),则向量





知识点
4.函数f(x)=2x+x-4的零点所在的区间为( )
正确答案
解析
对于连续函数f(x)=2x+x﹣4,由于f(1)=﹣1<0,f(2)=2>0,故函数f(x)=2x+x﹣4的零点所在的一个区间是(1,2),故选C.
知识点
5. 已知△ABC中,点D在BC边上,且
正确答案
解析
∵ △ ABC中,点D在BC边上,且









知识点
10. 一艘海轮从A处出发,以每小时40n mile的速度沿东偏南50°方向直线航行,30min后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是( )
正确答案
解析
知识点
3.已知a、b为实数,则“2a>2b”是“lna>lnb”的( )
正确答案
解析
由“2a>2b”得a>b,由“lna>lnb”得a>b>0,则“2a>2b”是“lna>lnb”的必要不充分条件,故选:B
知识点
8. 已知f(x)=
正确答案
解析
∵ 当x≤1时,f(x)=(4﹣


知识点
9. 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<)的图象如图所示,为了得到g(x)=cos2x的图象,则只要将f(x)的图象( )
正确答案
解析
由图象可知A=1,T=π,∴ω=














知识点
2.下列命题中是假命题的是( )
正确答案
解析
对于A,当φ=



知识点
12. 函数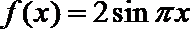
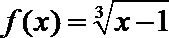
正确答案
解析
知识点
6.x=
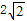
正确答案
解析
∵ x=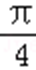
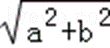
其中,cosθ=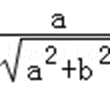
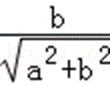
且函数f(x)的最大值为2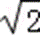
则a2+b2=8,f(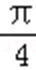


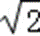


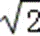
可得a+b=4,或a+b=﹣4,
∴a=b=2,或 a=b=﹣2,g(x)=2sinx+2,或g(x)=﹣2sinx﹣2,
故g(x)=asinx+b的最大值可能为0,故选:B.
知识点
11.数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*).若b3=-2,b10=12,则a8=( )
正确答案
解析
知识点
14.如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为_________ .
正确答案
解析
由题意,y=lnx与y=ex关于y=x对称,∴ 阴影部分的面积为2



知识点
13.设{an}是首项为a1,公差为﹣1的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则a1的值为_________。
正确答案
﹣
解析
由题意可得,an=a1+(n﹣1)(﹣1)=a1+1﹣n,Sn=
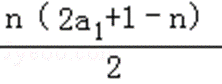
再根据若S1,S2,S4成等比数列,可得 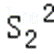
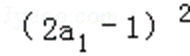
解得 a1=﹣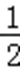
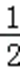
知识点
16. 给出下列四个命题:
①命题

②函数

③设





④定义在




⑤已知幂函数


其中真命题的序号是__________(把所有真命题的序号都填上)。
正确答案
③ ④ ⑤
解析
知识点
15.数列{an}通项公式an=2n sin(-)+ncos,前n项和为Sn,则S2015=__________。
正确答案
-1008
解析
知识点
19. 在△ABC中,角A,B,C的对边分别为a,b,c,且满足(a-c) 
(1)求角B的大小;
(2)若|

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知函数f(x)=cosx•sin(x+


(1)求f(x)的最小正周期;
(2)求f(x)在闭区间[﹣

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 数列



(1)求数列
(2) 记




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列{an}的首项a1=1,且满足
(1)设
(2)设cn=bn·2n,求数列{cn}的前n项和Sn.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 设函数f(x)=x3-x2+bx+c,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
(1)求b,c的值;
(2)若a>0,求函数f(x)的单调区间;
(3)设函数g(x)=f(x)+2x,且g(x)在区间(-2,-1)内存在单调递减区间,求实数a的取值范围.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)若函数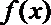
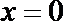
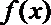
(2)是否存在实数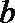
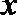
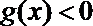
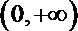
(3)证明:不等式
正确答案
解析
解析已在路上飞奔,马上就到!