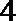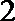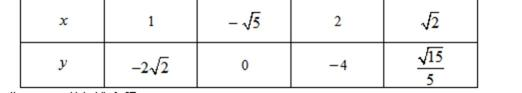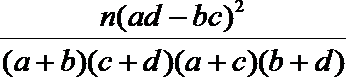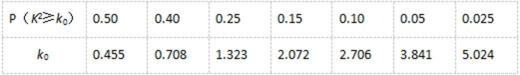- 真题试卷
- 模拟试卷
- 预测试卷
6.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知


(1)
(2)
(3)

(4)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知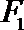
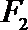
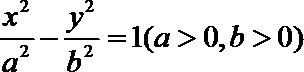
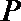
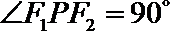
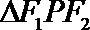
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在实数集

在平面向量集








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 条件




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知




值域为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.命题“对任意的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 右图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数和众数分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知非零向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 点













正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
12.把边长为1的正方形


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数





正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


(1)求函数
(2)已知横坐标分别为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆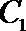
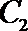

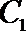

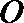
(1)求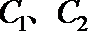
(2)过曲线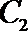
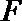
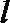
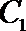
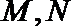
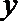
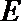
若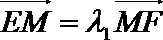
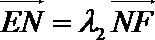
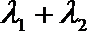
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.给定函数



(1)若函数




(2)在(1)的条件下,若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
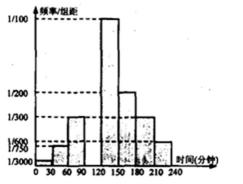
20.某校高一年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查。根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,l50),[150,180),[180,210),[210,240),得到频率分布直方图如下图。已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人。
(1)求n的值并求有效学习时间在[90,120)内的频率;
(2)如果把“学生晚上有效时间达到两小时”作为是
否充分利用时间的标准,对抽取的n名学生,请
补完整下列2×2列联表并判断是否有95%的把握
认为学生利用时间是否充分与走读、住宿有关?
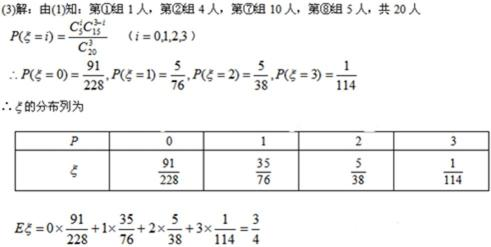
(3)若在第①组、第②组、第⑦组、第⑧组中共抽出3
人调查影响有效利用时间的原因,记抽到“有效学
习时间少于60分钟”的学生人数为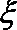
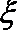
参考公式:K2=
参考列表:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某长方体截去一个三棱锥后,形成的几何体的平面展开图如图(1—1)所示。
(1)请在图(1—2)上补画出该几何体的直观图,并求出被截去的三棱锥的体积;
(2)在该几何体的直观图中连结


(3)在该几何体中求平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数





(1)求常数
(2)若存在


(3)对于函数







正确答案
解析
解析已在路上飞奔,马上就到!