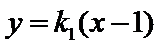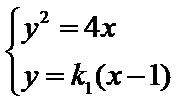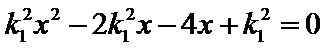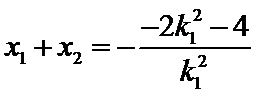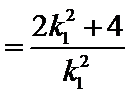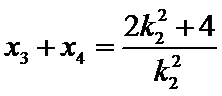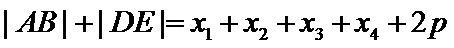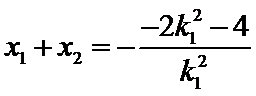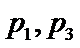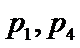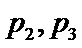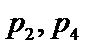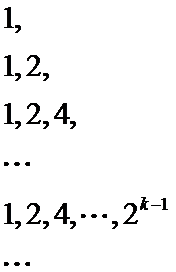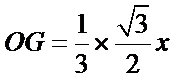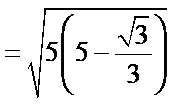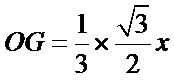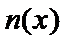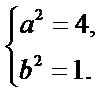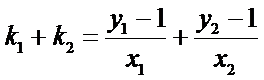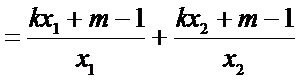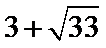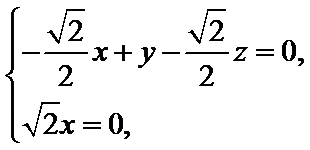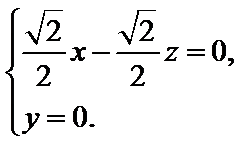- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={x|x<1},B={x|
正确答案
解析
由





考查方向
解题思路
应先把集合化简再计算,再直接进行交、并集的定义运算.
易错点
集合的交、并集运算灵活运用
5.函数




正确答案
解析
因为









考查方向
解题思路
由函数为奇函数且在



易错点
函数的奇偶性与单调性的综合应用
6.

正确答案
解析
因为








考查方向
解题思路
将第一个二项式中的每项乘以第二个二项式的每项,再分析好
易错点
准确分析清楚构成
9.已知曲线C1:y=cos x,C2:y=sin (2x+
正确答案
解析
因为








考查方向
解题思路
首先利用诱导公式将不同名函数转换成同名函数,
易错点
对变量
10.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
正确答案
解析
设直线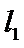
取方程
得
∴
同理直线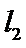
由抛物线定义可知
当且仅当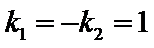
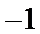
考查方向
解题思路
设直线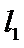
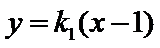
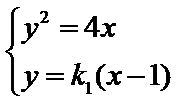
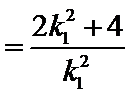
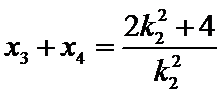
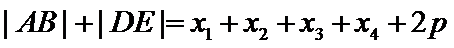
易错点
抛物线焦点弦公式
2.如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
正确答案
解析
设正方形边长为




考查方向
解题思路
正方形边长为



易错点
几何概型中事件A区域的几何度量
3.设有下面四个命题
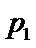
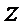
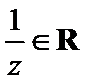
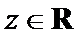
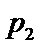
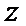
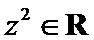
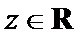
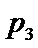
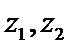
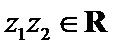
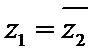
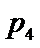
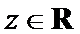
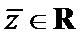
其中的真命题为( )
正确答案
解析
令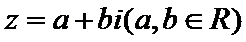
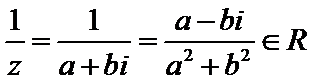
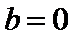
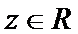
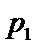
由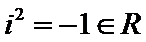
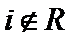
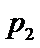
由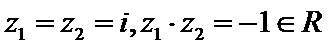
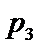
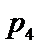
考查方向
解题思路
根据复数的分类,复数运算性质依次对每一个进行验证命题的真假,可得答案
易错点
真假命题的判断
4.记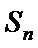
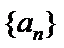
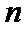
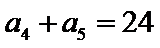
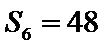
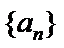
正确答案
解析
设公差为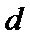
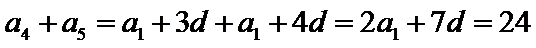
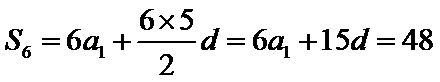
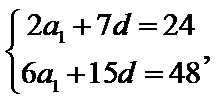
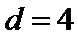
考查方向
解题思路
设公差为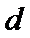
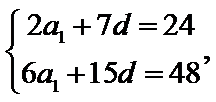
易错点
数列的基本量方程组的求解
7.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
正确答案
解析
由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为
考查方向
解题思路
由题意该几何体的直观图是由一个三棱锥和三棱柱构成,则该几何体各面内只有两个相同的梯形,由边的关系计算出梯形的面积之和
易错点
根据三视图判断几何体的形状及数据所对应的几何量
8.下面程序框图是为了求出满足3n−2n>1000的最小偶数n,那么在

正确答案
解析
由题意,因为




考查方向
解题思路
通过程序框图的要求,写出每次循环的结果得到输出的值.
易错点
循环结构的条件判断
11.设x、y、z为正数,且
正确答案
解析
令


∴



考查方向
解题思路
令





易错点
比较数的大小
12.几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
正确答案
解析
由题意得,数列如下:
则该数列的前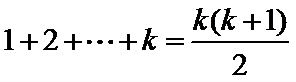
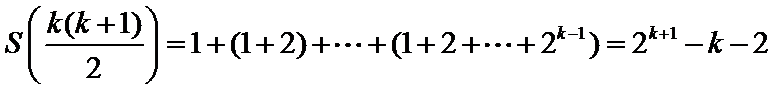
要使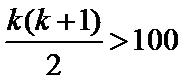
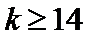
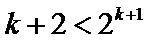
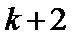
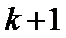
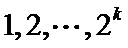
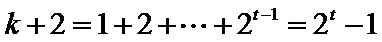
所以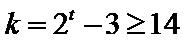
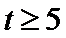
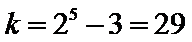
所以对应满足条件的最小整数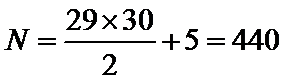
考查方向
等差数列、等比数列的求和.
解题思路
由题意列出数列,即为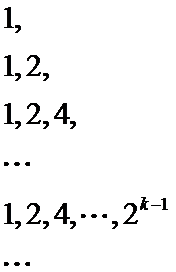
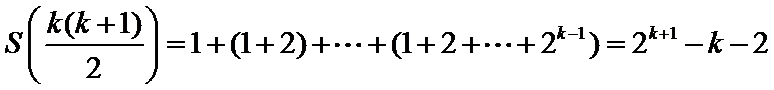
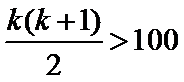
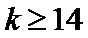
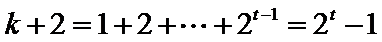
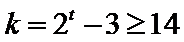
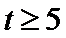
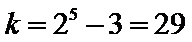
易错点
观察所给定数列的特征,进而求数列的通项和求和
13.已知向量a,b的夹角为60°,|a|=2,|b|=1,则| a +2b |= .
正确答案
解析


考查方向
解题思路
将| a +2b |平方得
易错点
平面向量中求模长的通常是见模平方
14.设x,y满足约束条件

正确答案
解析
不等式组表示的可行域如图所示,
易求得
由



所以,当直线


所以

考查方向
解题思路
作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到结论.
易错点
z的几何意义
15.已知双曲线C:
正确答案
解析
如图所示,作




而

点


在



由

所以
考查方向
解题思路








易错点
双曲线渐近线性质的灵活应用
16.如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .
正确答案
解析
如下图,设正三角形的边长为x,则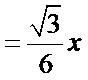
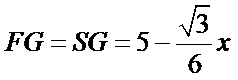
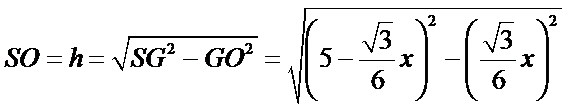
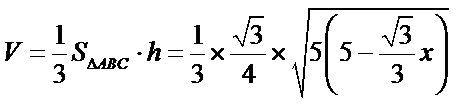
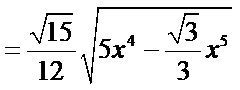
令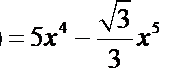
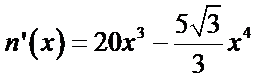
令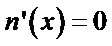
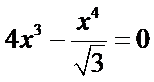
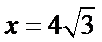
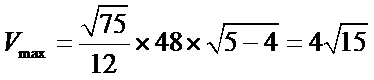
考查方向
解题思路
设正三角形的边长为x,则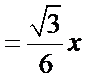
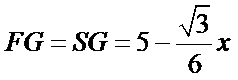
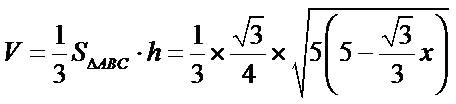
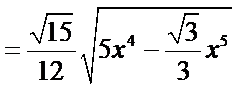
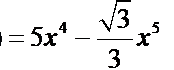
易错点
利用导函数求体积的最大值
20.(12分)
已知椭圆C: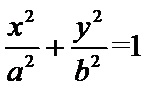
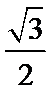
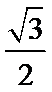
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
正确答案
(1)C的方程为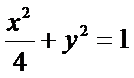
解析
(1)由于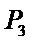
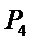
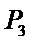
又由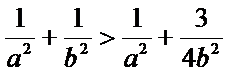
因此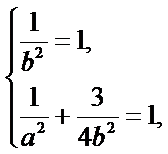
故C的方程为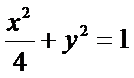
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知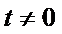
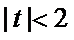
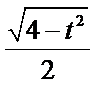
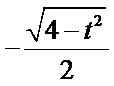
则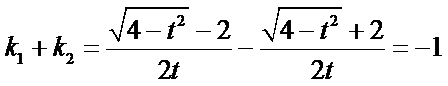
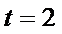
从而可设l: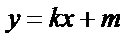
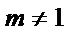
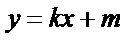
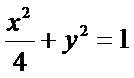
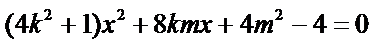
由题设可知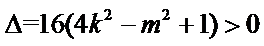
设A(x1,y1),B(x2,y2),则x1+x2=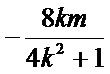
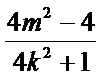
而
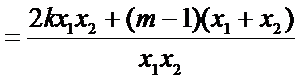
由题设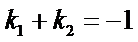
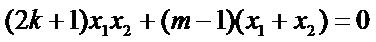
即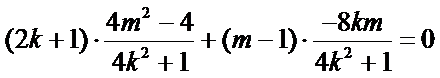
解得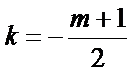
当且仅当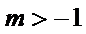
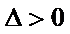
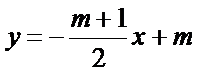
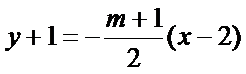
所以l过定点(2,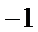
考查方向
解题思路
(1)由于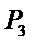
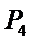
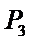
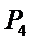
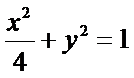
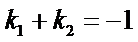
易错点
用根与系数的关系研究直线与圆锥曲线和关系
17.(12分)
△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为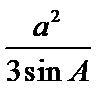
(1)求sin Bsin C;
(2)若6cos Bcos C=1,a=3,求△ABC的周长.
正确答案
(1)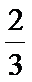
解析
(1)由题设得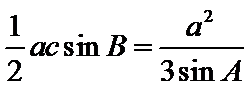
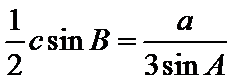
由正弦定理得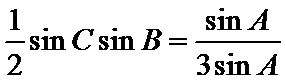
故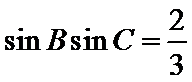
(2)由题设及(1)得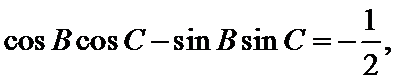
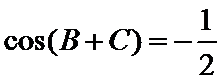
所以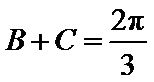
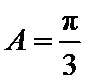
由题设得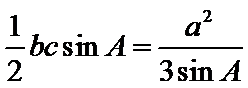
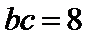
由余弦定理得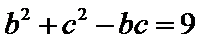
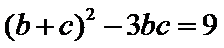
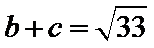
故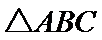
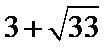
考查方向
解题思路
(1)由三角形面积公式建立等式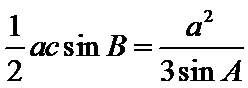
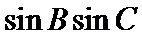
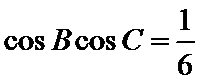
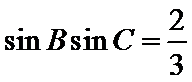
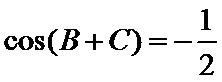
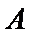
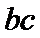
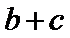
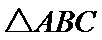
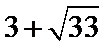
易错点
解三角形中正弦、余弦定理的灵活运用
18.(12分)
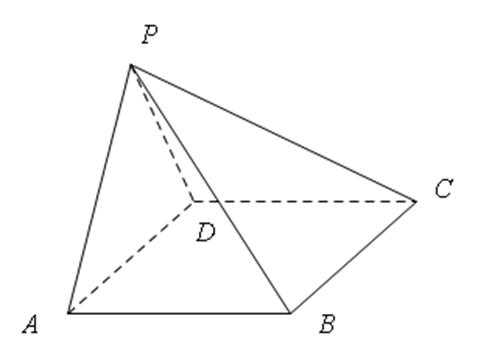
如图,在四棱锥P−ABCD中,AB//CD,且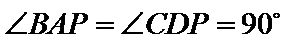
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,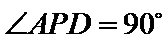
正确答案
(1)见解析;(2)
解析
(1)由已知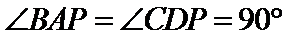
由于AB//CD ,故AB⊥PD ,从而AB⊥平面PAD.
又AB 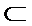
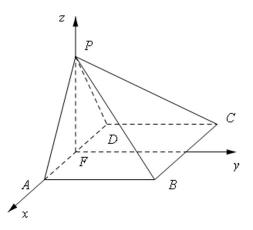
(2)在平面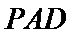
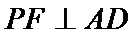
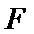
由(1)可知,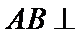
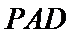
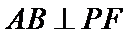
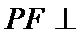
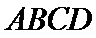
以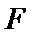
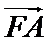
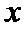
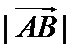
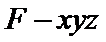
由(1)及已知可得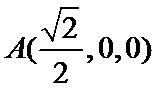
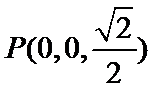
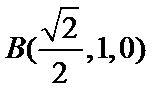
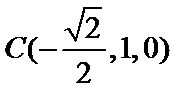
所以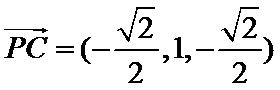
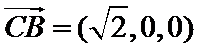
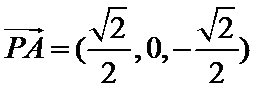
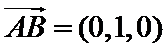
设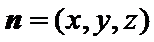
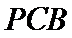
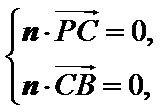
可取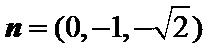
设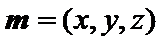
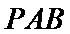
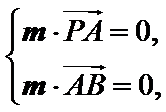
可取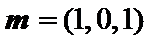
则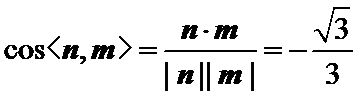
所以二面角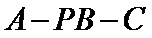
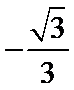
考查方向
解题思路
根据题设可以得出AB⊥AP,CD⊥PD,而AB//CD,就可证明出AB⊥平面PAD,进而证明平面PAB⊥平面PAD;(2)先找出AD中点,找出相互垂直的线,建立空间直角坐标系,列出所需要的点坐标,求出平面PCB,平面PAB的法向量,利用数量积求出二面角的平面角的余弦值
易错点
坐标法求两个半平面的法向量
19.(12分)
为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在


(2)一天内抽检零件中,如果出现了尺寸在
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
正确答案
解析
考查方向
(1)正态分布;(2)随机变量的期望和方差.
解题思路
易错点
随机变量的期望和方差的求解
21.(12分)
已知函数
(1)讨论
(2)若
正确答案
(1)见解析;(2)
解析
(1)


(ⅰ)若



(ⅱ)若


当






(2)(ⅰ)若

(ⅱ)若



①当


②当



③当


又


设正整数


由于


综上,

考查方向
解题思路
(1)讨论





















易错点
含参函数进行分类讨论其单调性
22.选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
[选修4−4:坐标系与参数方程](10分)
在直角坐标系xOy中,曲线C的参数方程为

(1)若a=−1,求C与l的交点坐标;
(2)若C上的点到l距离的最大值为
正确答案
(1)



解析
(1)曲线

当


由


从而



(2)直线





当




当




综上,

考查方向
解题思路
(1)曲线




易错点
用参数方程求曲线上点到直线最大距离
23.选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
[选修4−5:不等式选讲](10分)
已知函数

(1)当a=1时,求不等式
(2)若不等式
正确答案
(1)
解析
(1)当


当

当


当


所以

(2)当

所以



又






所以

考查方向
解题思路
(1)分区间去绝对值,然后分别解不等式,最后取并集即为原不等式的解集;(2)当



易错点
绝对值不等式的分段讨论