- 真题试卷
- 模拟试卷
- 预测试卷
2.若a,b是空间两条不同的直线,α,β是空间的两个不同的平面,则a⊥α的一个充分不必要条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数y=3x+1(-1≤x<0)的反函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知{an}是等比数列,a2=2,a5=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知定义域是全体实数的函数y=f(x)满足f(x+2π)=f(x),且函数g(x)=



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合M={x|x2-2x-3≤0,x∈R},N={x||x|<2,x∈R},则M∩N等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知两个向量a=(1,2),b=(x,1),若(a+2b)//(2a-2b),则x的值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一次演出,原计划要排4个节目,因临时有变化,拟再添加2个小品节目,若保持原有4个节目的相对顺序不变,则这6个节目不同的排列方法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知x,y满足条件,则x-y的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若n展开式的二项式系数之和为256,则n=______,其展开式的常数项等于_____.(用数字作答)
正确答案
8,70
解析
解析已在路上飞奔,马上就到!
知识点
11.在等差数列{an}中,已知a1+2a8+a15=96,则2a9-a10=________.
正确答案
24
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数y=2sin(2x+)的图象关于点P(x0,0)成中心对称,若x0∈[-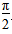
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设i为虚数单位,则复数=________.
正确答案
-1+i
解析
解析已在路上飞奔,马上就到!
知识点
13.以双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB、CD的长度分别为2和4,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB、CD可能相交于点M;
②弦AB、CD可能相交于点N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正确命题的序号为______.
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
16.将3封不同的信投进A、B、C、D这4个不同的信箱、假设每封信投入每个信箱的可能性相等.
(Ⅰ)求这3封信分别被投进3个信箱的概率;
(Ⅱ)求恰有2个信箱没有信的概率;
(Ⅲ)求A信箱中的信封数量的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设定义在R上的函数f(x)=a0x4+a1x3+a2x2+a3x+a4(a0,a1,a2,a3,a4∈R)当x=-1时,f(x)取得极大值,且函数y=f(x+1)的图象关于点(-1,0)对称.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)试在函数y=f(x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-

(Ⅲ)设xn=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知F1,F2分别是椭圆


(Ⅰ)求曲线C的方程;
(Ⅱ)证明:

(Ⅲ)若λ∈[2,3],求|PQ|的取值范围.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,已知四棱锥P-ABCD的底面是菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD.
(Ⅰ)求证:PD⊥BC;
(Ⅱ)若AB=6,PC=6,求二面角P-AD-C的大小;
(Ⅲ)在(Ⅱ)的条件下,求异面直线PB与DE所成角的余弦值.
正确答案
解:解法一:(Ⅰ)在菱形ABCD中,连接DB,则△BCD是等边三角形.
∵点E是BC边的中点 ∴DE⊥BC. ∵PO⊥平面ABCD,
∴OD是斜线PD在底面ABCD内的射影.∴PD⊥BC.
(Ⅱ)由(Ⅰ)知DE⊥BC,菱形ABCD中,AD∥BC,
∴DE⊥AD. 又∵PO⊥平面ABCD,DE是PD在平面ABCD的射影,
∴PD⊥AD. ∴∠PDO为二面角P-AD-C的平面角.
在菱形ABCD中,AD⊥DE,由(1)知,△BCD为等边三角形,
∵点E是BC边的中点,AC与BD互相平分, ∴点O是△BCD重心.
∵AB=6, 又∵在等边△BDC中, DO=DE=·BC=×6=6. ∴OC=OD=6.
∵PC=6,∴PO=6. ∴在Rt△POD中,tan∠PDO===1.∴∠PDO=.
∴二面角P-AD-C的大小为.
(Ⅲ)
取AD中点H,连接HB,HP. 则HB∥DE.
∴HB与PB所成角即是DE与PB所成角. 连接OH,OB.
∵PO⊥平面ABCD,OH,OB⊂平面ABCD,
∴PO⊥OH,PO⊥OB. 在Rt△DOH中,HD=3,OD=6,
∴OH=3. 在Rt△PHO中,PH==. 在Rt△POB中,OB=OC=6,PB==6
由(Ⅱ)可知DE=HB=9. 设HB与PB所成角为α, 则cosα==.
∴异面直线PB、DE所成角的余弦值为.
解法二:(Ⅰ)同解法一;
(Ⅱ)过点O作AD平行线交AB于F,以点O为坐标原点,建立如图的坐标系.
∴A(6,-6,0),B(3,3,0),C(-3,3,0), D(0,-6,0),P(0,0,6).
∴

设平面PAD的一个法向量为s=(a,m,n).
则
∵

∴二面角P-AD-C的大小为.
(Ⅲ)由已知,可得点E(0,3,0).
∴

∴cos〈

解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数f(x)=sinωx·cosωx-cos2ωx(ω>0)的最小正周期为.
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时f(x)的值域.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}中,a1=t(t∈R,且t≠0,1),a2=t2,且当x=t时,函数f(x)=
(Ⅰ)求证:数列{an+1-an}是等比数列;
(Ⅱ)若bn=anln|an|(n∈N),求数列{bn}的前n项和Sn;
(Ⅲ)当t=-
正确答案
解析
解析已在路上飞奔,马上就到!