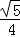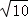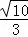- 真题试卷
- 模拟试卷
- 预测试卷
6.(1-x)2(1+y)3的展开式中xy2的系数是
正确答案
解析
略。
知识点
7.设x,y满足约束条件


正确答案
解析
略。
知识点
1.已知集合M={y|y=x2﹣1,x∈R},N={x|y=
正确答案
解析
略。
知识点
10.某同学在研究函数f(x)=



①f(x)的图象是中心对称图形;
②f(x)的图象是轴对称图形;
③函数f(x)的值域为
④函数f(x)在区间(﹣∞,3)上单调递减;
⑤方程
上述关于函数f(x)的描述正确的个数为( )
正确答案
解析
略。
知识点
2.已知i为虚数单位,若数列{an}满足:a1=i,且(1﹣i)an+1=(1+i)an,则复数a5=( )
正确答案
解析
略。
知识点
3.已知{an}为等比数列,下面结论中正确的是( )
正确答案
解析
略。
知识点
4.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①m⊥α,n∥α,则m⊥n;
②若α⊥γ,β⊥γ,则α∥β;
③若α∥β,β∥γ,m⊥α,则m⊥γ;
④若α∩γ=m,β∩γ=n,m∥n,则α∥β。
其中正确命题的序号是( )
正确答案
解析
略。
知识点
9.过双曲线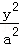
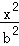
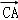
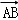
正确答案
解析
略。
知识点
5.定义











正确答案
解析
略。
知识点
8.已知关于x的方程|x﹣k|=

正确答案
解析
略。
知识点
11.某班有60名学生,一次考试后数学成绩ξ~N(110,102),若P(100≤ξ≤110)=0.35,则估计该班学生数学成绩在120分以上的人数为________。
正确答案
9
解析
略。
知识点
16.若实数x,y,z满足x2+y2+z2=4,则x+2y﹣2z的取值范围为________。
正确答案
[-6,6]
解析
略。
知识点
13.执行如图所示的程序框图,若输出结果是i=3,则正整数a0的最大值为________。
正确答案
3
解析
略。
知识点
15.已知AB是半圆O的直径,点C在半圆上,CD⊥AB于点D,且AD=4DB,设∠COD=θ,则cos2θ=________。
正确答案
-
解析
略。
知识点
12.(x2+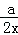
正确答案
解析
略。
知识点
14.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。若曲线C1的参数方程为
正确答案
1
解析
略。
知识点
17.设a∈R,

(1)求函数f(x)的单调递增区间;
(2)设△ABC三内角A,B,C所对边分别为a,b,c且
正确答案
(1)
(2)(-1,2]
解析
(1)f(x)=asinxcosx﹣cos2x+sin2x=
由

因此
令
得
故函数f(x)=的单调递增区间
(2)由余弦定理知:
即2acosB﹣ccosB=bcosC,
又由正弦定理知:2sinAcosB=sinCcosB+sinBcosC=sin(B+C)=sinA
即
当

故f(x)在(0,B]上的值域为(-1,2]
知识点
18.2014年巴西世界杯的周边商品有80%左右为“中国制造”,所有的厂家都是经过层层筛选才能获此殊荣.甲、乙两厂生产同一产品,为了解甲、乙两厂的产品质量,以确定这一产品最终的供货商,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及其均值(即数学期望)。
正确答案
见解析。
解析
(1)乙厂生产的产品总数为5
(2)样品中优等品的频率为
乙厂生产的优等品的数量为35×
(3)由题意知ξ=0,1,2,
P(ξ=0)=

P(ξ=1)=

P(ξ=2)=
ξ的分布列为
均值Eξ=1×0.6+2×0.1=0.8
知识点
19.如图,正四棱锥S﹣ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点。
(l)求证:EP⊥AC;
(2)当直线BP与平面EFG所成的角取得最大值时,求二面角P﹣BD﹣C的大小。
正确答案
见解析。
解析
(1)证明:设AC交BD于O,
∵S﹣ABCD为正四棱锥,∴SO⊥底面ABCD,
∴SO⊥AC,
又∵BD⊥AC,SO∩BD=O,
∴AC⊥平面SBF,∴AC⊥SO,
∵SD∥FG,∴AC⊥GF,又AC⊥GE,∴AC⊥平面GEF,
又∵PE⊂面GEF,∴PE⊥AC
(2)解:设AB=2,如图建立空间直角坐标系,
则G(0,1,0),E(1,0,0),C(1,1,0),
S(0,0,



∴
设
∴
设面EFG的法向量为
∵
∴

设BP与平面EFG所成角为α,
则
∵点P在线段FG上,∴0≤λ≤1,即λ=1时sinα取最大值
此时点P与点F重合
设二面角P﹣BD﹣C的大小为θ
∵点P到平面ABCD的距离为
则
∴二面角P﹣BD﹣C的大小为45°
知识点
20.设{an}为公比不为1的等比数列,a4=16,其前n项和为Sn,且5S1、2S2、S3成等差数列.
(l)求数列{an}的通项公式;
(2)设bn=

正确答案
见解析。
解析
(1)设{an}为公比q不为1的等比数列,
∵5S1、2S2、S3成等差数列,
∴4S2=5S1+S3,即
∴q2﹣3q+2=0,
∵q≠1,∴q=2,
又∵a4=16,即
∴
(2)假设存在正整数k使得对于任意n∈N*不等式
则
又
∴
显然Tn关于正整数n是单调递增的,
∴
∴
∴存在正整数k,使得对于任意n∈N*不等式
知识点
21.设椭圆C1:
(1)求椭圆C1的方程;
(2)设M(0,
正确答案
(1)
(2)
解析
(1)由题意可知B(0,﹣1),则A(0,﹣2),故b=2
令y=0得x2﹣1=0即x=±1,则F1(﹣1,0),F2(1,0),故c=1
所以a2=b2+c2=5
于是椭圆C1的方程为:
(2)设N(t,t2﹣1),由于y'=2x知直线PQ的方程为:y﹣(t2﹣1)=2t(x﹣t)
即y=2tx﹣t2﹣1
代入椭圆方程整理得:4(1+5t2)x2﹣20t(t2+1)x+5(t2+1)2﹣20=0,
△=400t2(t2+1)2﹣80(1+5t2)[(t2+1)2﹣4]=80(﹣t4+18t2+3),


故
=
设点M到直线PQ的距离为d,则
所以,△MPQ的面积S=
=
当t=±3时取到“=”,经检验此时△>0,满足题意
综上可知,△MPQ的面积的最大值为
知识点
22.已知函数g(x)=alnx,f(x)=x3+x2+bx。
(1)若f(x)在区间[1,2]上不是单调函数,求实数b的范围;
(2)若对任意x∈[1,e],都有g(x)≥﹣x2+(a+2)x恒成立,求实数a的取值范围;
(3)当b=0时,设F(x)=
正确答案
见解析。
解析
(1)由f(x)=x3+x2+bx
得f'(x)=3x2+2x+b因f(x)在区间[1,2]上不是单调函数
所以f'(x)=3x2+2x+b在[1,2]上最大值大于0,最小值小于0,
∴-16<b<-5
(2)由g(x)≥﹣x2+(a+2)x,得(x﹣lnx)a≤x2﹣2x
∵x∈[1,e],∴lnx≤1≤x,且等号不能同时取,∴lnx<x,即x﹣lnx>0
∴a≤
令

当x∈[1,e]时,x﹣1≥0,0≤lnx≤1x+2﹣2lnx>0,从而f′(x)≥0,
∴f(x)在[1,e]上为增函数,∴
∴a≤﹣1
(3)由条件,F(x)=
假设曲线y=F(x)上存在两点P,Q满足题意,
则P,Q只能在y轴两侧,…(9分)
不妨设P(t,F(t)),t>0则Q(﹣t,t3+t2),且t≠1
∵△POQ是以O为直角顶点的直角三角形,
∴
∴﹣t2+F(t)(t3+t2)=0 (*),
是否存在P,Q等价于方程(*)在t>0且t≠1时是否有解
①若0<t<1时,方程(*)为﹣t2+(﹣t3+t2)(t3+t2)=0,
化简得t4﹣t2+1=0,此方程无解
②若t>1时,方程(*)为﹣t2+alnt(t3+t2)=0,
即
设h(t)=(t+1)lnt,(t>1),则h′(x)=lnt+
显然,当t>1时,h′(x)>0,即h(x)在(1,+∞)上为增函数,
∴h(t)的值域为(h(1),+∞),即(0,+∞),
∴当a>0时,方程(*)总有解
∴对任意给定的正实数a,曲线y=F(x) 上总存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上。