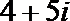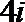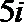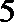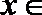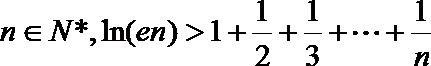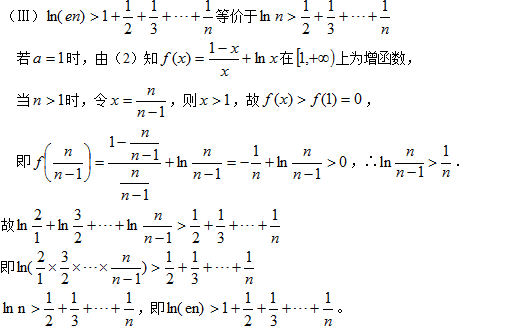- 真题试卷
- 模拟试卷
- 预测试卷
2.设复数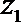
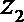
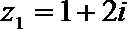
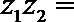
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.下列说法正确的是（ ）
A命题“若x2＝1，则x＝1”的否命题为“若x2＝1，则x≠1”
B命题“∀x≥0，x2＋x－1＜0”的否定是“∃x0＜0，x＋x0－1≥0”
C命题“若x＝y，则sin x＝sin y”的逆否命题为假命题
D若“
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.若
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.已知全集U＝R，集合A＝{1，2，3，4，5}，B＝[3，＋∞)，则图中阴影部分所表示的集合为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.设函数f(x)(x∈R)满足f(x＋2)＝f(x)＋2．当0≤x<2时，f(x)＝1，则f(2014)＝（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7.设函数
①
②
③
④
其中正确的结论个数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8.如图，对于曲线Ψ所在平面内的点O，若存在以O为顶点的角α，使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A.B恒成立，则称角α为曲线Ψ的相对于点O的“界角”，并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”．已知曲线C：
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.
正确答案
7
解析
解析已在路上飞奔，马上就到！
知识点
10.
正确答案
π2―2
解析
解析已在路上飞奔，马上就到！
知识点
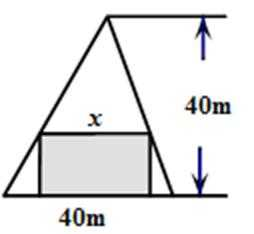
13.在如图所示的锐角三角形空地中, 欲建一个面积不小于300m2的内接矩形花园(阴影部分), 则其边长x(单位m)的取值范围是__________.
正确答案
[10，30]
解析
解析已在路上飞奔，马上就到！
知识点
12.若函数
正确答案
(－2，2)
解析
解析已在路上飞奔，马上就到！
知识点
14.已知真命题:“函数
正确答案
(－1，1)
解析
解析已在路上飞奔，马上就到！
知识点
11.已知函数
正确答案
(－∞，2]∪[5，＋∞)
解析
解析已在路上飞奔，马上就到！
知识点
19.已知函数
（1）若
（2）求函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20.已知函数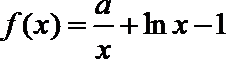
（I）若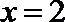
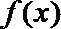
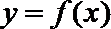
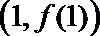
（II）当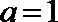
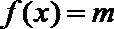
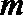
（III）求证:
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15.已知函数
（1）求函数
（2）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16.如图, 
（1）求证：
（2）求二面角
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.某公司从一批产品中随机抽出60件进行检测. 下图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100)，[100，102)，[102，104)，[104，106].
（1）求图中
（2）若将频率视为概率，从这批产品中有放回地随机抽取3件，求至多有2件产品的净重在[96，98）的概率；
（3）若产品净重在[98，104)为合格产品，其余为不合格产品. 从这60件抽样产品中任选2件，记
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18.某商场销售某件商品的经验表明，该商品每日的销量
（1）求实数
（2）若该商品的成本为3元/千克，试确定销售价格
正确答案
解析
解析已在路上飞奔，马上就到！