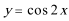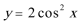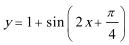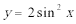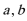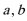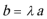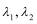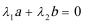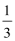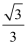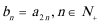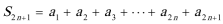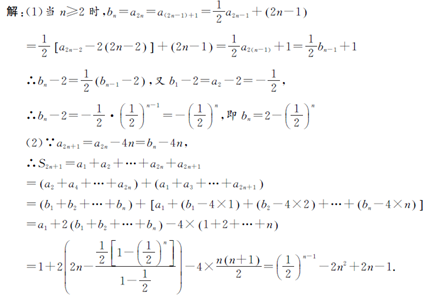- 真题试卷
- 模拟试卷
- 预测试卷
5.在极坐标中,由三条曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.将函数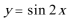
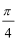
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知二次函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
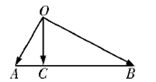
2.平面向量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知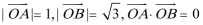

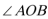
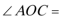

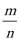
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.用0.618法选取试点,实验区间为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 函数



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 直线


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
15. 已知数列




正确答案
4.5,32
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量


(1)求

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列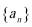
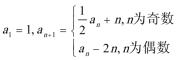
(1)求数列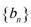
(2)求和
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.函数





(1)求

(2)求

(3)若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在



(1)判断
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5千美元~8千美元的地区销售该公司
(1)下列几个模拟函数中




①
③

(2)若人均GDP为1千美元时,年人均


(3)因为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设数列
(1)当


(2)当

(i)
(ii)
正确答案
解析
解析已在路上飞奔,马上就到!