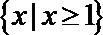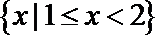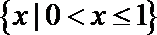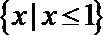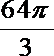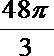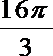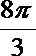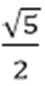- 真题试卷
- 模拟试卷
- 预测试卷
5．数列{an}是公差不为0的等差数列，且a6、a9、a15依次为等比数列{bn}的连续三项，若数列{bn}的首项b1＝
A
B
C31
D32
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．某路段的雷达测速区检测点，对过往汽车的车速进行检测所得结果进行抽样分析，并绘制如图所示的时速（单位km/h）频率分布直方图，若在某一时间内有200辆汽车通过该检测点，请你根据直方图的数据估计在这200辆汽车中时速超过65km/h的约有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
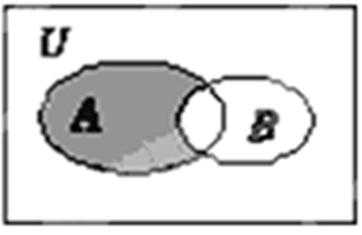
1．设全集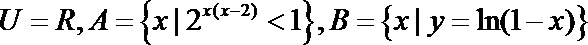
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．现有5本不同的书，全部分给四个学生，每个学生至少1本，不同分法的种数为 （ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
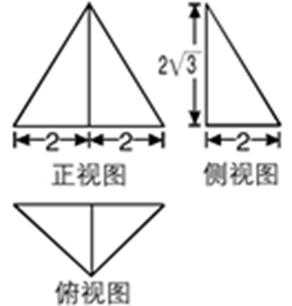
8．一个几何体的三视图如图所示，其中正视图是正三角形，则该几何体的外接球的表面积为 （ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．如图，在一个长为π，宽为2的矩形OABC内，曲线y＝sin x(0≤x≤π)与x轴围成如图所示的阴影部分，向矩形OABC内随机投一点(该点落在矩形OABC内任何一点是等可能的)，则所投的点落在阴影部分的概率是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．若直线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．抛物线
A
B
C1
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12． 已知定义在R上的可导函数
A
B
C
D不确定
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．函数
正确答案
解析
解析已在路上飞奔，马上就到！
13．若
正确答案
20
解析
解析已在路上飞奔，马上就到！
知识点
15．已知双曲线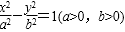
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．在长方体ABCD－A1B1C1D1中，AB＝2，BC＝AA1＝1，则D1C1与平面A1BC1所成角的正弦值为_________。
正确答案
1/3
解析
解析已在路上飞奔，马上就到！
知识点
17．已知Sn为数列{an}的前n项和，且2an＝Sn＋n．
（1）若bn＝an＋1，证明：数列{bn}是等比数列；
（2）求数列{Sn}的前n项和Tn。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．
（1）求证：AA1⊥平面ABC；
（2）求二面角A1-BC1-B1的余弦值；
（3）证明：在线段BC1上存在点D，使得AD⊥A1B，并求
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．某学校为了丰富学生的业余生活，以班级为单位组织学生开展古诗词背诵比赛，随机
抽取题目，背诵正确加10分，背诵错误减10分，只有“正确”和“错误”两种结果，
其中某班级的正确率为
（1） 求
（2）记
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知椭圆C：
（1）求椭圆的方程；
（2）设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（1）求函数
（2）若函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
选考题（从下列三道解答题中任选一题做答，若多做，则按首做题计入总分）。
22．选修4－1：几何证明选讲
如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，EC＝ED．
（1）证明：CD∥AB；
（2）延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G，F四点共圆．
23．选修4－4：坐标系与参数方程
已知直线
（1）设与
（2）若把曲线
24．选修4—5：不等式选讲
设
（1）当a=5，解不等式
（2）当a=1时，若
22．选修4－1：几何证明选讲
如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，EC＝ED．
（1）证明：CD∥AB；
（2）延长CD到F，延长DC到G，使得EF＝EG，
证明：A，B，G，F四点共圆．
23．选修4－4：坐标系与参数方程
（1）设
（2）若把曲线
24．选修4—5：不等式选讲
设
（1）当
（2）当
