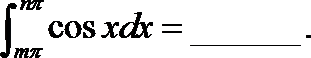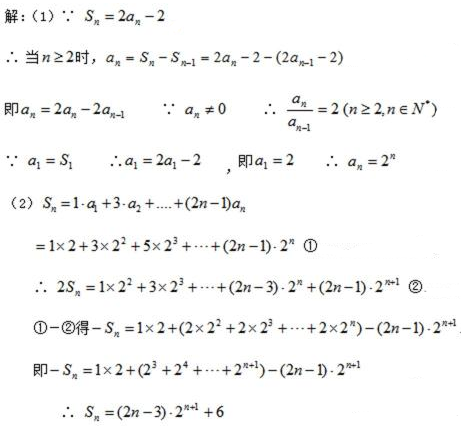- 真题试卷
- 模拟试卷
- 预测试卷
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4 .函数y=lgx-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.自然数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知两个非零向量








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.集合



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11. 等比数列




正确答案
126
解析
解析已在路上飞奔,马上就到!
知识点
13. 在锐角



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数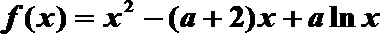
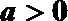
(1)当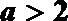
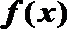
(2)当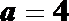
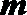
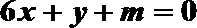

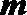
(3)设定义在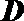
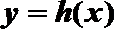
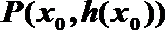
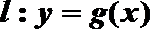
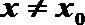
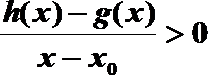
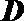
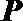
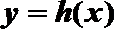
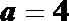

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知正方形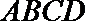
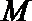
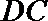
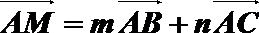
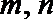
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
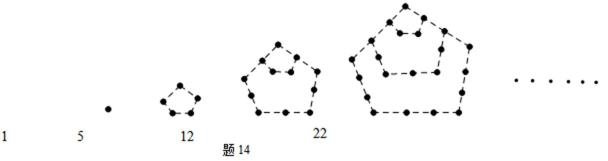
14. 两千多年前,古希腊毕达哥拉

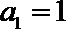







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知向量


(1)求
(2 )求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,简单组合体ABCDPE,其底面ABCD为边长为

(1)若N为线段PB的中点,求证:EN//平面ABCD;
(2)求点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列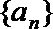

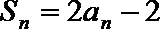
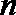
(1)求数列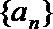
(2)记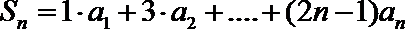
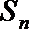
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为



(1)求S关于x的函数关系式及该函数的定义域;
(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列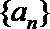



(1)求数列
(2)设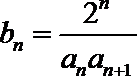




正确答案
解析
解析已在路上飞奔,马上就到!