- 真题试卷
- 模拟试卷
- 预测试卷
1.当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设点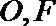
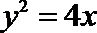
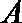
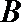
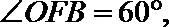
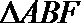
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 在平面直角坐标系中,若角




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”。下列四个命题,其中是“可换命题”的是( )
①垂直于同一平面的两直线平行
②垂直于同一平面的两平面平行
③平行于同一直线的两直线平行
④平行于同一直线的两平面平行
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 用反证法证明命题:“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 下列命题中错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 如图,四棱锥






(Ⅰ)求证:

(Ⅱ)当二面角


(Ⅲ)在(Ⅱ)的条件下,求直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知双曲线

(Ⅰ) 求双曲线
(Ⅱ)已知点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数




(I) 如果函数



(Ⅱ)设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知数列




(Ⅰ)求数列
(Ⅱ)求数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知

(Ⅰ) 求函数
(Ⅱ)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 把离心率相同的椭圆叫做“相似椭圆”,如图的两个相似椭圆,分别是同一个矩形的内切椭圆和外接椭圆,且
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
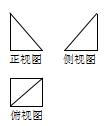
12.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若要拼成一个棱长为1的正方体,则需要这样的几何体( )个。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,由若干个点组成形如长方形的图形,每条边(包括两个端点)有

正确答案
解析
解析已在路上飞奔,马上就到!