- 真题试卷
- 模拟试卷
- 预测试卷
2.已知集合


正确答案
解析
由已知解出


因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
先解出集合B,再求出

易错点
对指数不等式的解法出错。
知识点
3.若双曲线的顶点和焦点分别为椭圆
正确答案
解析
由椭圆方程





因此B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
根据已知椭圆方程写出其焦点和顶点坐标,从而知双曲线的顶点和焦点坐标,由此确定a,b,c的值最后给出双曲线的方程。因此B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
易混淆椭圆与双曲线中a,b,c之间的关系以及a,b,c在两种曲线中所表示的意义。
知识点
4.现有



正确答案
解析
法一:2黑2白或3黑1白或4黑的结果数分别为







考查方向
解题思路
直接法:至少有2个黑球的取法有2黑2白或3黑1白或4黑三种情况
间接法:先算出10个球取出4个的总实验结果数,再计算全白或者3白1黑的实验结果数,再两数结果相减得到答案。因此A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
至少问题出现少算或者多算或重复算的情况。
知识点
8.执行如图所示的程序框图,则输出结果
正确答案
解析
当n=1时a=

考查方向
解题思路
先分别列出当n取1,2,3.....时a对应的值,并从中找到n与a取值的循环规律,从而得到答案。
易错点
做循环结构的程序框图试题时,一定要注意输出的条件,否则会造成失误。
知识点
9.已知函数


正确答案
解析
由已知得






考查方向
解题思路
先化简得



易错点
三角函数在某个给定区间递增或递减,不能正确转化满足条件的不等式。
知识点
10.如图,网格纸上小正方形的边长为
正确答案
解析
根据三视图还原成几何体如图所示,该四面体的表面积为
因此A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
根据三视图还原几何体为一个三棱锥,由图中数据可算出该四面体的表面积。
易错点
不能通过左视图中的虚线(实线)构想出其中一个顶点的位置而出错。
知识点
6.定义在







正确答案
解析
由







考查方向
解题思路
由题意知f(x)是以2为周期的函数,又由




易错点
1、不能正确处理

知识点
1.若

正确答案
解析
由




因此A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据


易错点
化简z时易出错
知识点
5.某工厂对新研发的一种产品进行试销,得到如下数据表:
根据上表可得回归直线方程


正确答案
解析
由表格知


考查方向
解题思路
通过表格算出

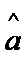
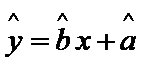
易错点
x,y任取某组给定值代入计算
知识点
7.在等比数列




正确答案
解析
在等比数列








考查方向
解题思路
在等比数列






易错点
由
知识点
11.已知函数




正确答案
解析
由






因此A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
由已知求出f(x)的解析式,由函数


易错点
1、不会求f(x)的表达式,2,不能通过图像法去理解两个函数的交点个数问题。
知识点
12.在公差不为







正确答案
解析
在等差数列中由








因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
1.在等差数列中由






易错点
求
知识点
13.已知向量




正确答案
解析
由已知得


考查方向
解题思路
要求





易错点
不能理解什么样的向量可作基底。
知识点
14.若



正确答案
5
解析
由已知x,y满足的不等式组所表示的可行域如图所示
所以在点A处时
考查方向
解题思路
首先画出不等式组表示的可行域,
易错点
不等式所表示的平面区域易出错,导致可行域出错。
知识点
15.已知三棱锥




正确答案
12
解析
由已知得当PA,PB,PC两两互相垂直时三棱锥
O’为正



考查方向
解题思路
由已知得当PA,PB,PC两两互相垂直时三棱锥
易错点
1、三个侧面面积之和最大不能转化;2,给定一个正三棱锥不知如何寻找内接球半径。
知识点
16.已知直线






正确答案
解析
根据椭圆参数方程设出B点坐标(acost,bsint),由
从而得出点P 
又



考查方向
解题思路
根据椭圆参数方程设出B点坐标(acost,bsint),由





易错点

知识点
如图,在四棱锥





19.求证:
20.若平面



正确答案
(1)

解析
试题分析:本题属于立体几何线面平行证明及二面角的余弦值的求解问题,属于中档题。
(Ⅰ)证明:取




∴
∵
∴
∵




∴平面

∵
∴

考查方向
解题思路
(1)通过面面平行证明线面平行;
(2)根据已知条件建立空间直角坐标系,用空间向量的方法求二面角的余弦值。
易错点
1)证明过程遗漏直线相交的条件
2)没有描述建系的依据,或点的坐标出错或运算出错。
正确答案
(2)所求二面角的余弦值为
解析
试题分析:本题属于立体几何线面平行证明及二面角的余弦值的求解问题,属于中档题。
(Ⅱ)解:









如图所示.
则点




设平面
则

设平面
因此所求二面角的余弦值为
考查方向
解题思路
(1)通过面面平行证明线面平行;
(2)根据已知条件建立空间直角坐标系,用空间向量的方法求二面角的余弦值。
易错点
1)证明过程遗漏直线相交的条件
2)没有描述建系的依据,或点的坐标出错或运算出错。
某种机器在一个工作班的8小时内,需要工作人员操控累计2个小时才能正常进行,当机器需用操控而无人操控时,机器自动暂停运行。每台机器在某一时刻是否用人操控彼此之间相互独立
21.若在一个工作班内有4台相同机器,求在同一时刻需用人操控的平均台数;
22.若要求一人操控的所有机器正常运行的概率控制在不低于




正确答案
(1)
解析
试题分析:本题属于概率问题,属于基础题,意在考查考生对基本概念的理解。
(Ⅰ)用




考查方向
解题思路
(1)用二项分布求数学期望
(2)首先要理解n取1,2,3时是属于什么概率问题,根据情况求出工作人员待工而闲的概率。
易错点
审题不清,不会用数学知识来转化。
正确答案
(2)一个工作人员操控2台机器符合要求
解析
试题分析:本题属于概率问题,属于基础题,意在考查考生对基本概念的理解。
(Ⅱ)设

①当

此时,一人操控1台机器,工作人员能够及时操控机器,不会出现机器等待操控的情形,但工作人员待工而闲的概率为
②当



此时,一人操控2台机器,在同一时刻需要操控2台机器的概率为



③当



此时,一人操控3台机器,出现机器等待工作人员操控而不能正常运行的概率为


综上所述,一个工作人员操控2台机器符合要求.
考查方向
解题思路
(1)用二项分布求数学期望
(2)首先要理解n取1,2,3时是属于什么概率问题,根据情况求出工作人员待工而闲的概率。
易错点
审题不清,不会用数学知识来转化。
已知抛物线









23.求
24.若圆




正确答案
(1)抛物线

解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅰ)设

又∵以


∴




考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


正确答案
(2)直线

圆
解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅱ)设直线


化简整理得
∴


∴圆心

∵圆


∴
∴

此时直线


圆心

圆

考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


在



17.求
18.若




正确答案
(1)
解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅰ)由正弦定理,
可得
所以
所以
因为


考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
正确答案
(2)

解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅱ)解法一:由已知
所以


当

所以
所以


因为

在

当
所以

(Ⅱ)解法二:在


因为

由已知

又
解得
考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
设函数



25.求
26.证明:
正确答案
(1)

解析
试题分析: 本题属于导数的综合应用,考查考生转化与化归数学思想与方法。
(Ⅰ)因为


又点


所以

考查方向
解题思路
(1)利用导数解决曲线的切线问题,从而解出a,b的值
(2)通过构造新函数的方法找到证明不等式的突破口。
易错点
不等式证明如何构造新函数
正确答案
(2)对任意

解析
试题分析: 本题属于导数的综合应用,考查考生转化与化归数学思想与方法。
(Ⅱ)令
因为

所以




我们如果能够证明

下面证明:对任意

由(1)知
则


又



当



当



所以


所以
令
所以

所以
综上,对任意

考查方向
解题思路
(1)利用导数解决曲线的切线问题,从而解出a,b的值
(2)通过构造新函数的方法找到证明不等式的突破口。
易错点
不等式证明如何构造新函数
【选修4-1:几何证明选讲】
如图,点







27.证明:弧

28.若

正确答案
(1)弧

解析
试题分析:本题属于圆与三角形基本性质的应用,较基础。
(Ⅰ)证明:∵
∴
∵
∴
∵
∴
∴
∴
∴
考查方向
解题思路
(1)由


(2)利用相似三角形的相似比得出答案。
易错点
圆及三角形的性质应用出错。
正确答案
(2)
解析
试题分析:本题属于圆与三角形基本性质的应用,较基础。
(Ⅱ)由(Ⅰ)知
∴
∴
又∵

∴
考查方向
解题思路
(1)由


(2)利用相似三角形的相似比得出答案。
易错点
圆及三角形的性质应用出错。
































































































































