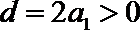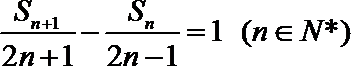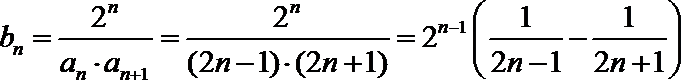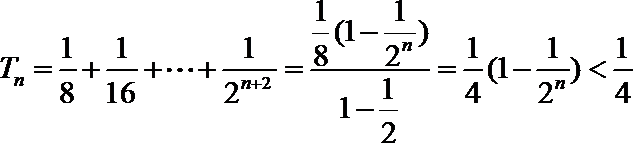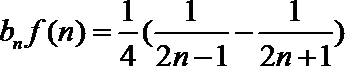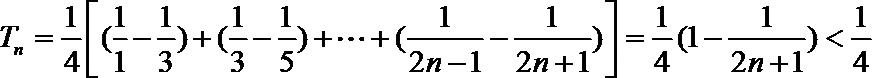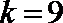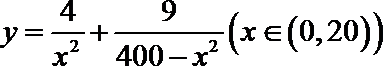- 真题试卷
- 模拟试卷
- 预测试卷
2.行列式

正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.有2本不同的数学书和3本不同的英语书分给五位同学,每人一本,则甲、乙两位同学恰有一位分到数学书的概率( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.程序框图(即算法流程图)如图所示,其输出结果是_______.
正确答案
127
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
10.正项无穷等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,半圆直径AB为6,点C为半圆弧上任意一点,图中阴影部分绕直线AB旋转一周所得旋转体的体积的最小值是( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.给定两个长度为1的平面向量






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.观察如图类似杨辉三角的数表,则此表最后一个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若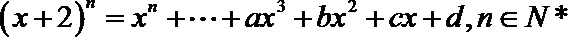
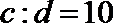
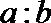
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
16.设矩形的长为




甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知直线l、m、n及平面
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在半径为3的球面上有





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.定义:如果一个向量列从第二项起,每一项与它的前一项的差都等于同一个常向量,那么这个向量列叫做等差向量列,这个常向量叫做等差向量列的公差.
已知向量列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设向量
(1)若


(2)若
正确答案
(1)∵

∴
∴
(2)
即
解析
解析已在路上飞奔,马上就到!
知识点
22.已知




(1)求出

(2)若

(3)解不等式:
正确答案
(1)由题意得
(2)

当函数

当函数
∴当


(3)∵
∴

① 当

② 当
③ 当

④ 当
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,在四棱锥






(1)求三棱锥
(2)求二面角
正确答案
(1)∵


∴

∴
(2)解:过点


















从而

由题设可得,




于是在

所以二面角

解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列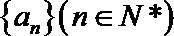
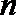
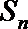
(1)当数列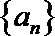
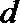
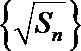
(2)若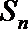
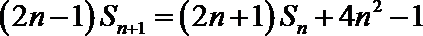
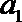
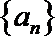
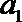
(3)若数列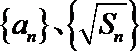
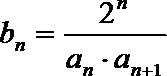
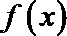
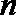
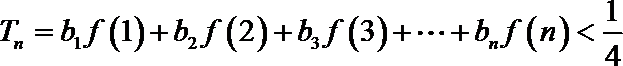
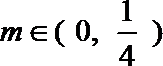
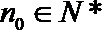
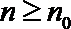
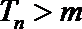
正确答案
(1)数列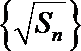
(2)∵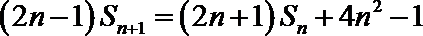
∴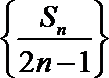
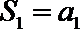
∴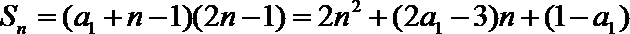
当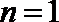
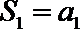
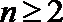
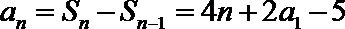
∵数列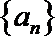
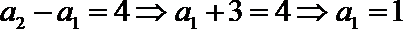
∴存在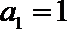
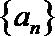
(3)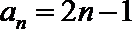
构造①:令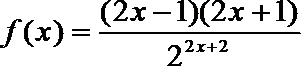
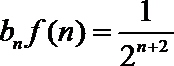
若
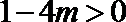
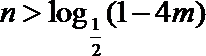
∴令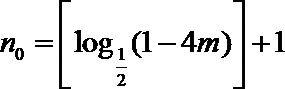
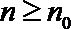
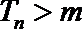
构造②:令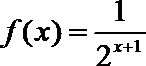
若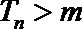
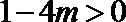
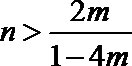
∴令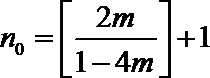
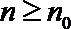
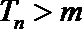
解析
解析已在路上飞奔,马上就到!
知识点
21.两城市A和B相距20km,现计划在两城市外以AB为直径的半圆弧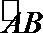
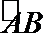
(1)将y表示成x的函数;
(2)判断弧
正确答案
(1)由题意得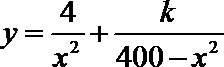
又∵当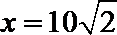
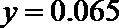
∴
∴
(2)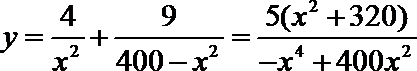
令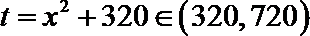
则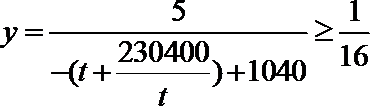
当且仅当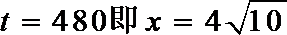
∴弧AB上存在一点,该点到城A的距离为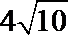
解析
解析已在路上飞奔,马上就到!