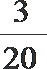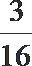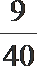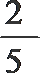- 真题试卷
- 模拟试卷
- 预测试卷
1．i 是虚数单位，复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知O为坐标原点，双曲线
A2
B3
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．下面四个条件中，使
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知圆
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5. 已知等比数列{
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6. 把五个标号为1到5的小球全部放入标号为1到4的四个盒子中，并且不许有空盒，那么任意一个小球都不能放入标有相同标号的盒子中的概率是 （ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．将
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11. 如果执行下面的框图，那么输出的S等于___________.
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
12. 已知
正确答案
π
解析
解析已在路上飞奔，马上就到！
知识点
15.选做题，从下面三题中选做一题。
（1)(不等式选讲）已知函数
(2)（极坐标与参数方程选讲）直角坐标系xOy中，圆C的参数方程是
(3)（几何证明选讲）如图，过点
正确答案
（1）
（2）
（3）
解析
解析已在路上飞奔，马上就到！
知识点
14. 若对于函数
①b=0时，
②y=
③b=－1时，方程
④b=－1时，不等式
其中正确的命题是______．（写出所有正确命题的编号）
正确答案
①②④
解析
解析已在路上飞奔，马上就到！
知识点
13. 设P是不等式组
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
16.已知函数
（Ⅰ）求数列
（Ⅱ）令
正确答案
（1）
当
(2)由（1) 得
解析
解析已在路上飞奔，马上就到！
知识点
18. 正
在图形（2）中：
（Ⅰ）试判断直线AB与平面DEF的位置关系，并说明理由；
（Ⅱ）求二面角E-DF-C的余弦值；
（Ⅲ）在线段BC上是否存在一点P，使
正确答案
（Ⅰ）如图（2）：在
又
（Ⅱ）以点D为坐标原点，以直线DB、DC、DA分别为x轴、y轴、z轴，
建立空间直角坐标系，则
平面CDF的法向量
设平面EDF的法向量为
则
（Ⅲ）在平面坐标系
则
∵
∴在线段BC上存在点P，使AP⊥DE.
解析
解析已在路上飞奔，马上就到！
知识点
19. 在抽样方法中，有放回抽样与无放回抽样中个体被抽到的概率是不同的，但当总体的容量很大而抽取的样本容量很小时，无放回抽样可以近似看作有放回抽样。现有一大批产品，采用随机抽样的方法一件一件抽取进行检验。若抽查的4件产品中未发现不合格产品，则停止检查，并认为该批产品合格；若在查到第4件或在此之前发现不合格产品，则也停止检查，并认为该批产品不合格。假定该批产品的不合格率为0.1，设检查产品的件数为X。
(Ⅰ) 求随机变量X的分布列和数学期望；
(Ⅱ) 通过上述随机抽样的方法进行质量检查，求认为该批产品不合格的概率。
正确答案
（1）由题意得，X的可能值为1,2,3,4，
则有
分布列略。EX=3.439.
（2）认为该批产品合格的概率是
从而该批产品不合格的概率是P=1-
解析
解析已在路上飞奔，马上就到！
知识点
20．已知中心在原点，焦点在坐标轴上的椭圆
(Ⅰ)求椭圆
(Ⅱ)若在椭圆
(Ⅲ)记点C为(Ⅱ)中直线AB恒过的定点，问否存在实数
正确答案
（I）设椭圆方程为
所以
（II）设切点坐标为
则切线方程分别为
又两切线均过点M，即
故直线AB的方程是
故直线AB恒过定点
（III）将直线AB的方程
得
所以
所以
即
解析
解析已在路上飞奔，马上就到！
知识点
21. 已知函数
(Ⅰ)若
(Ⅱ)若对任意x∈[1，e]，都有
(Ⅲ)在(Ⅰ)的条件下，设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17. 如图，港口A北偏东30°方向的C处有一检查站，港口正东方向的B处有一轮船，距离检查站31海里，该轮船从B处沿正西方向航行20海里后到达D处观测站，已知观测站与检查站距离21海里，问此时轮船离港口A还有多远？
正确答案
在△BDC中，由余弦定理知cos∠CDB＝
sin∠CDB＝
∴轮船距港口A还有15海里．
解析
解析已在路上飞奔，马上就到！