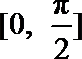- 真题试卷
- 模拟试卷
- 预测试卷
4.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数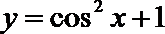
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知幂函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.向量a,b满足|a|=1,|a-b|=,a与b的夹角为60°,则|b|=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设












正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合A={x|-x2-3x>0},B={x|x<-1},则A∩B=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知非零向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在平行四边形ABCD中,AC与BD交于O,E是线段OD的中点,AE的延长线与CD交于点F,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知向量a与b的夹角为,且|a|=1,|b|=4,若(2a+λb)⊥a,则实数λ=________.
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,函数g(x)=-x3+2x2+mx+5在(-∞,+∞)内单调递减,则实数m等于________.
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
13.直线









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.有一道解三角形的题目,因纸张破损有一个条件模糊不清,具体如下:“在△




正确答案


解析
解析已在路上飞奔,马上就到!
知识点
12.若数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14~15题,只能从中选做一题)
14.(坐标系与参数方程)
直角坐标系
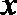
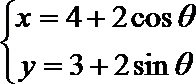
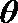
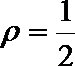
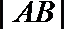
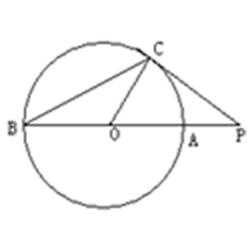
15.(几何证明选讲)
如图,
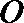
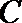
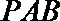
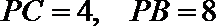
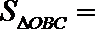
正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥








(Ⅰ)当


(Ⅱ) 当二面角



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以



(Ⅲ)是否存在实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知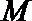
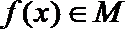
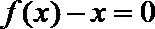
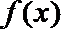
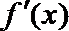
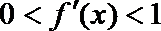
(Ⅰ)集合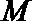
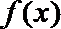
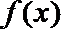
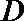
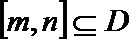
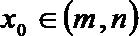
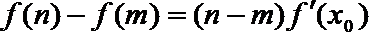
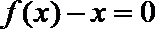
(Ⅱ)对任意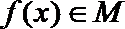
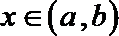
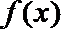
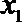
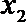
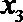
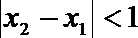
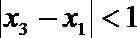
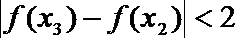
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在锐角







(Ⅰ)求
(Ⅱ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品。用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量



(Ⅰ)求函数


(Ⅱ)在








正确答案
解析
解析已在路上飞奔,马上就到!