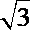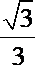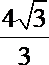- 真题试卷
- 模拟试卷
- 预测试卷
1.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
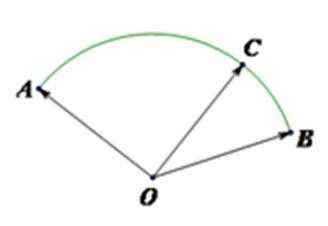
8.如图,半径为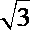
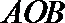
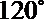
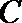
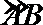
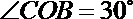
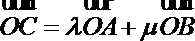
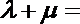
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.动圆



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一支田径队有男运动员 56人,女运动员 42 人,若用分层抽样的方法从全体运动员中抽出一个容量为 28 的样本,则样本中男运动员的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知一元二次不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对于平面直角坐标系内任意两点


①若


②若点


③在

④若



⑤若




正确答案
①②⑤
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,直角









正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.设



正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
18.已知

(Ⅰ)求证:
(Ⅱ)求函数

正确答案
解:(Ⅰ)因为

得:


当且仅当

(Ⅱ)由(Ⅰ)知,
当且仅当


解析
解析已在路上飞奔,马上就到!
知识点
21.设









(Ⅰ)用


(Ⅱ)求证:
(Ⅲ)设


正确答案
解:(Ⅰ)由点


又点在圆

从而




将

(Ⅱ) 

又

所以 
(Ⅲ)先证:当

不等式
后一个不等式显然成立,而前一个不等式
故当




求和得:

解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(Ⅰ)设


(Ⅱ)求函数
正确答案
(Ⅰ)由题知


所以

故


当

(Ⅱ)由题知

所以

解析
解析已在路上飞奔,马上就到!
知识点
17.前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(Ⅲ)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记

正确答案
解:(Ⅰ)众数:8.6;中位数:8.75 ;
(Ⅱ)设

则
(Ⅲ)





所以
另解:
则



解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆







(Ⅰ)求椭圆
(Ⅱ)设



正确答案
(Ⅰ)依题意,




所以椭圆的标准方程为
(Ⅱ)由椭圆定义知

而


当且仅当



所以

设



解得



解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)若

(Ⅱ)试问:对某个实数



正确答案
解:(Ⅰ)定义域为

则当



当



故函数

(Ⅱ)假设方程

设


则
即

则
设



则当



则


则
故不存在.
解析
解析已在路上飞奔,马上就到!