- 真题试卷
- 模拟试卷
- 预测试卷
6.已知圆






正确答案
解析





考查方向
本题主要考查了直线与圆的位置关系问题,属于中档题,是高考的热点,解决此类题的关键会用直线与圆的位置关系计算弦长。
易错点
本题易在计算弦长时发生错误,导致题目错误。
知识点
8.已知正方体






正确答案
解析
由图可知过点A三条直线


考查方向
本题主要考查了立体几何中异面直线所成角及直线和平面所成角,属于中档题,是高考的热点,解决此类题的关键:找出三条直线所成角都相等的直线条数。点与三个平面所成角都相等的直线的条数。
易错点
1、本题易在找点

知识点
1.已知

正确答案
解析


考查方向
本题主要考查了复数的乘法运算、复数的相等,属于简单题,是高考的热点,解决此类题的关键:是会进行复数的乘法运算。
解题思路
无
易错点
本题易在复数相等时错误,等式左右两边都写成a+bi形式,导致题目出现错误
知识点
2. 抛物线

正确答案
解析
抛物线

考查方向
本题主要考查了抛物线的几何性质,属于简单题,是高考的热点,解决此类题的关键是记住抛物线的准线方程。
易错点
本题易在记忆抛物线的准线方程出错。
知识点
3.如图,正方形




正确答案
解析



考查方向
本题主要考察了平面向量的基本定理,属于中档题,是高考的热点,解决此类题的关键是会利用平面向量的基本定理,用两个不共线的向量表示平面内任一向量。
易错点
本题易在向量的表示过程中出现错误。
知识点
4.某程序框图如图所示,执行该程序,若输入的

正确答案
解析
按照程序框图进行运算,当i=1时,a=1;当i=2时,a=3;当i=3时,a=3;当i=4时.i>3输出a=3
考查方向
本题主要考查了程序框图,属于中档题,是高考的热点,解决此类题的关键读懂程序框图,并按步骤写出其过程。
易错点
本题易在写过程时发生错误。
知识点
5.已知数列



正确答案
解析
由



考查方向
本题主要考察了排列组合的知识,属于中档题,是高考的热点,解决此类题的关键:找到

易错点
本题易在
知识点
7.若


正确答案
解析
线性目标函数
考查方向
本题主要考察了线性规划,属于中档题,是高考的热点,解决此类题的关键:正确的画出可行域,并理解目标函数的意义。
易错点
1、本题易在画可行域时发生错误
2、本题不容易理解
知识点
10. 在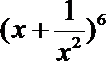
正确答案
15
解析
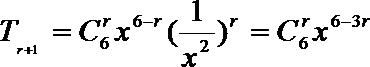
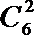
考查方向
本题主要考察了二项式定理中的指定项的问题,属于中档题,是高考的热点,解决此类题的关键:用二项式定理中的通项,让x的次数为0。
易错点
本题易在用二项式定理中的通项时发生错误,导致题目无法进行。
知识点
9.已知双曲线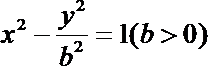
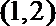
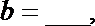
正确答案
2;
解析
双曲线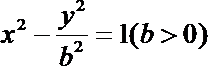
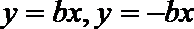
易错点
本题易在记忆双曲线的渐近线方程时发生错误从而导致b值的错误。
知识点
11.已知等比数列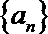
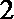

正确答案
6
解析
由题意可得,

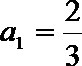
易错点
本题易在计算首项时发生错误,从而导致题目结果出现错误。
知识点
13.已知函数


正确答案
-4
解析
解析已在路上飞奔,马上就到!
易错点
本题易在理解分段函数性质时发生错误,导致题目无法进行。
知识点
12. 某四棱锥的三视图如图所示,则该四棱锥中最长棱的棱长为
正确答案
解析
由三视图可知是如图正方体的一部分,所以可知其最长棱为
易错点
本题易在由三视图画原图时发生错误,导致题目无法进行。
知识点
14.已知




(i) 在满足下述条件的三角形中,存在“友好”三角形的是____:(请写出符合要求的条件的序号)
①
②
③
(ii) 若等腰
正确答案
②;
解析







考查方向
本题主要考察了解三角形问题,属于难题,是高考的热点,解决此类题的关键:一是会化简,熟悉三角恒等变形公式;二是会用性质,熟悉单解三角形的问题。
易错点
本题易在公式变形时发生错误,导致题目出错。
知识点
16.已知某种动物服用某种药物一次后当天出现A症状的概率为
(Ⅰ)如果出现A症状即停止试验”,求试验至多持续一个用药周期的概率;
(Ⅱ)如果在一个用药周期内出现3次或4次A症状,则这个用药周期结束后终止试验,试验至多持续两个周期. 设药物试验持续的用药周期数为

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)设持续


所以
则
法二:设用药持续最多一个周期为事件

所以
所以
(Ⅱ)随机变量

所以

所以
考查方向
本题主要考察了概率统计,期望的问题,属于中档题,是高考的热点,解决此类题的关键:会用公式算概率和期望。
易错点
1、本题易在读题时因读不懂题意,导致概率无法计算。
2、因期望中随机变量对应的概率算错而导致出错。
知识点
17.







(Ⅰ)若点


证明:

(Ⅱ)求二面角
(Ⅲ)在线段


若存在,求出
正确答案
见解析
解析
(Ⅰ)过点




因为

又


所以

又






(Ⅱ)因为梯形



因为


如图,以


所以
设平面



因为
所以

取

同理可得
所以
因为二面角
所以二面角

(Ⅲ)假设存在点

所以
所以

所以存在点
考查方向
本题主要考察了立体几何中的线面平行,二面角和存在性问题,属于中档题,是高考的热点,解决此类题的关键:一是熟悉定理进行证明线面平行;二是向量法解决二面角的问题。
易错点
1、本题易在证明线面平行时,条件不全面。
2、本题可能在算法向量时易错,导致题目结果出错。
知识点
18.已知函数
(Ⅰ)当

(Ⅱ)求证:当



(其中
正确答案
(Ⅰ)函数



(Ⅱ)见解析
解析
(Ⅰ)因为
所以
当

令
得
所以

所以




函数




(Ⅱ)证明:不等式

等价于

即函数

因为
令

因为

当


函数

所以函数


所以不等式

当


所以函数



此时

所以

综上,当



考查方向
本题主要考察了用导数解决函数的单点区间和极值的问题,属于中档题,是高考的热点,解决此类题的关键:
1、(1)确定函数y=f(x)的定义域;
(2)求导数y′=f′(x);
(3)解不等式f′(x)>0,解集在定义域内的部分为单调递增区间;
(4)解不等式f′(x)<0,解集在定义域内的部分为单调递减区间.
2、当函数f(x)在点x0处连续时,①如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值;②如果在x0附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x0)是极小值。
易错点
1、导数为零的点不一定是极值点 。
2、本题对k的分类讨论不全面导致错误。
知识点
15.已知函数
(Ⅰ)求函数
(Ⅱ)求函数

正确答案
(Ⅰ)
(Ⅱ)0
解析
(Ⅰ)因为



(Ⅱ)因为


当


当


因为
所以函数

考查方向
本题主要考察了三角函数的图象与性质,属于中档题,是高考的热点,解决此类题的关键:一是会化简,熟悉三角恒等变形公式;二是会用性质,熟悉单调性、周期性、对称性、和最值问题。
易错点
1、本题易在化简的过程汇总发生错误,导致最小正周期算错 。
2、单调性分析不全面,导致题目无法进行。
知识点
19.




(Ⅰ)求椭圆
(Ⅱ)若点



的另一个交点为


若存在,求出点
正确答案
(Ⅰ)
(Ⅱ)不存在
解析
(Ⅰ)因为椭圆


令


又离心率为


所以
所以

(Ⅱ)法一



与椭圆方程联

化简得到
因为
所以
所以
所以
因为圆心到直线

所以
因为
代入得到
显然


法二:设点


与椭圆方程联立得
化简得到


显然
所以另一个根,
即
由
因为圆心到直线

所以
因为
代入得到
若


所以不存在直线

法三:假设存在点



显然直线


由

由

所以
同理可得
所以由

则

所以不存在直线

考查方向
本题主要考察了椭圆的方程与直线与椭圆的位置关系问题:
一是会用待定系数法求椭圆的方程;
二是会用熟悉用根与系数的关系解决直线和圆锥曲线的位置关系问题。
易错点
1、本题易在用待定系数法用错导致圆锥曲线方程算错。
2、本题用根与系数的关系时运算出错导致后面全部错误。
知识点
20.若实数数列



(1)若数列




(2) 求证:若数列


(3) 若数列






正确答案
(1)
(2)见解析
(3)
解析
(1)因为

所以
所以
所以

所以
(2) 假设


所以

故

假设

则

故

(3)由(Ⅱ)可知

且最多连续两项都是负数,最多连续三项都是正数.
因此存在最小的正整数


设


故有

由上可知


因为
所以当

当



记


当



此时

若


此时

当



综上可知

考查方向
本题主要考察了数列中项的问题,属于难题,是高考的热点,解决此类题的关键:是会对数列中的项进行分析。
易错点
1、本题易在对数列中的项分析不全面出现错误 。
2、对数列中项的性质研究不全面出现错误。