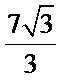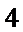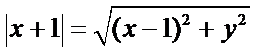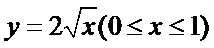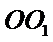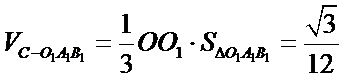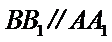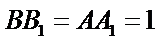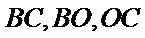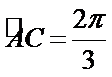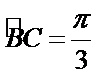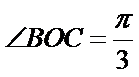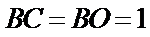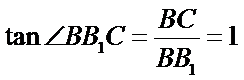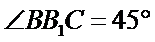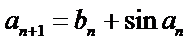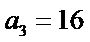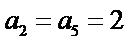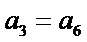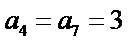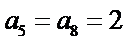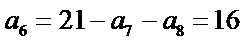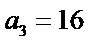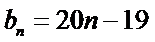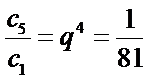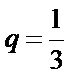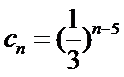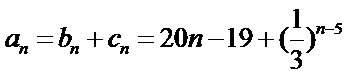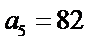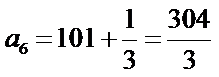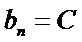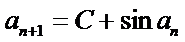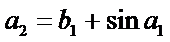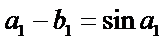- 真题试卷
- 模拟试卷
- 预测试卷
8.在

正确答案
解析


通项
取
常数项为
考查方向
解题思路
利用二项式系数和先求得项数,然后写出通项公式,最后确定常数项并化简.
易错点
二项式展开的通项公式以及常数项的确定.
知识点
9.已知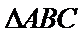
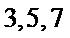
正确答案
解析
不妨设三边分别为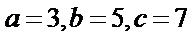
由余弦定理可得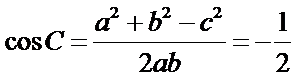
∴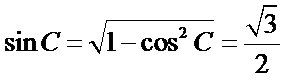
∴由正弦定理可得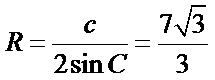
考查方向
解题思路
已知三边长,先由三角形的余弦定理求得其中一角的余弦值,再根据同角三角比的平方关系求得这个角的正弦值,最后利用三角形的正弦定理,求得该三角形外接圆的半径.
易错点
恰当合理运用正弦定理和余弦定理.
知识点
2.设


正确答案
解析

考查方向
解题思路
先通过复数运算化简得到

易错点
复数
知识点
3.




正确答案
解析


考查方向
解题思路
将相关数值直接代入两平行直线距离公式
易错点
计算错误.
知识点
4.某次体检,

正确答案
解析
将数据按从小到大排列:


考查方向
解题思路
首先将数据按从小到大排列,然后找到最中间的两个数(因为原始数据有偶数个),求得它们的平均数即可.
易错点
对偶数个数据时中位数的计算.
知识点
5.已知点



正确答案
解析
将点


故
∴
∴
∴
考查方向
解题思路
先将点



易错点
对数函数的正确表达形式.
知识点
6.如图,在正四棱柱




正确答案
解析
∵

∴

在



∴

考查方向
解题思路
先确定



易错点
正确寻找直线与平面所成的角.
知识点
10.设



正确答案
解析
由已知,有
又


考查方向
解题思路
先利用行列式确定方程组无解的充要条件,然后利用基本不等式求得
易错点

知识点
7.方程

正确答案

解析


∴
∴
∴
考查方向
解题思路
利用三角公式先将三角方程化为最简形式,然后求最简单的三角方程.
易错点
合理恰当的选择三角公式化简三角方程.
知识点
1.设

正确答案
解析



考查方向
解题思路
先去绝对值,然后利用不等式性质移项即可.
易错点
绝对值不等式的等价形式.
知识点









正确答案
解析
任取不同的两个点

符合要求的有序点对

∴符合要求的点

考查方向
解题思路
先确定分母,八个点任取不同的两个点的种数为


易错点
枚举法寻找符合要求的有序点对
知识点
12.在平面直角坐标系中,已知




正确答案
解析
设



∴
考查方向
解题思路
先设半圆曲线






易错点
正确设动点

知识点
11.无穷数列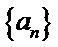
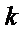
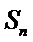
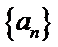
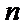
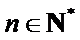
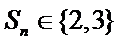
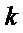
正确答案
解析
根据题意,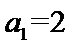
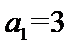
∵
∴从第二项开始,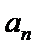
由题意无穷数列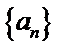
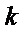
那么在同一个数列中,它们只可能是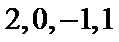
∴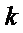
考查方向
易错点
没有厘清关系,无从着手.
知识点
13.设




正确答案
解析
①当
若



②当
若



共
考查方向
解题思路
根据三角函数的性质,枚举有序实数组
易错点
在枚举过程中漏考虑若干情形.
知识点
17.已知无穷等比数列





正确答案
解析



若

若

考查方向
解题思路
先将无穷等比数列前


易错点
对化简之后
知识点
16.下列极坐标方程中,对应的曲线为右图的是 ( )
正确答案
解析
本题可以采用排除法,当

显然符合要求的选项为D.
考查方向
解题思路
利用
易错点

15.设


正确答案
解析
设


由子集与推出关系可知“

考查方向
解题思路
利用子集与推出关系求解.
易错点
子集与推出关系.
知识点
18.设

①若



②若





下列判断正确的是 ( )
正确答案
解析
①不成立,可举反例


②
前两式作差,可得
结合第三式,可得
也有
故选D.
考查方向
解题思路
不成立的举反例,成立的要证明.
易错点
反例找不到.
知识点
有一块正方形菜地















21.求菜地内的分界线
22.菜农从蔬菜运量估计出










正确答案
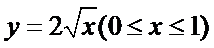
解析
设分界线上任一点为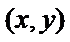
可得
考查方向
解题思路
根据抛物线定义或者直接列式得到曲线方程;
正确答案
矩形面积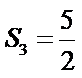
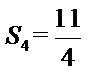
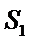
解析
设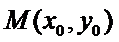
∴
∴设所表述的矩形面积为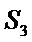
过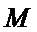
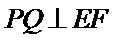
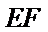
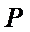
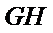
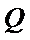
设五边形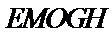
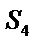
∵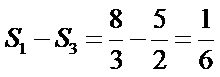
∴五边形
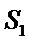
考查方向
解题思路
分别求得矩形和五边形的面积,然后求得其与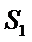
易错点
对“更接近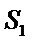
将边长为
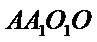
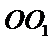
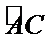
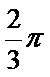
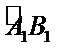
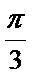
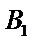
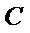
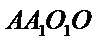
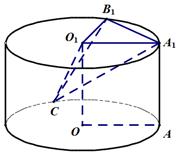
19.求三棱锥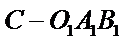
20.求异面直线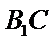
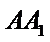
正确答案
解析
连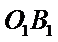
∴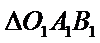
∴
又三棱锥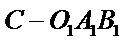
∴
考查方向
解题思路
确定三棱锥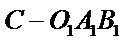
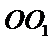
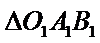

易错点
三棱锥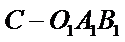
正确答案
解析
设点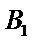
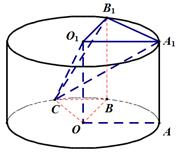
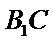
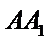
连
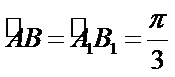
∴
∴
∴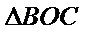
∴
∴
∴
∴直线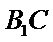
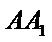
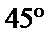
考查方向
解题思路
利用平行,找到直线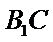
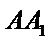
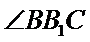
易错点
在圆柱体内找直线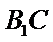
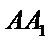
双曲线





23.若


24.设



正确答案
解析
由已知
取
∵
∴
即
∴
∴渐近线方程为
考查方向
解题思路
利用等边三角形及双曲线相关知识求双曲线方程;
易错点
计算错误
正确答案
解析
若
∴
设



∴

∵
∴
∴代入(*)式,可得
直线
∴
设直线

得
∴
∴
∴
∴直线
考查方向
解题思路
利用向量运算、直线与圆锥曲线位置关系、二次方程根与系数关系计算求解.
易错点
向量关系进行转化
已知

25.当

26.若关于


27.设





正确答案

解析
∴不等式的解集为
考查方向
解题思路
利用对数函数性质、不等式性质求解对数不等式
易错点
函数性质的综合运用.
正确答案


解析
依题意,
∴
可得
即
当

当

当


若

若

要使得方程①有且仅有一个解,则
综上,若原方程的解集有且只有一个元素,则


考查方向
解题思路
先去对数符号,将对数方程等价转化为关于
易错点
函数性质的综合运用.
正确答案

解析


依题意,
即
∴
设
当
当
∵函数

∴
∴
∴
考查方向
解题思路
利用函数单调性将问题转化为我们熟悉的不等式的在给定范围的恒成立,然后分离参数转化为
易错点
函数性质的综合运用.
若无穷数列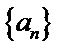

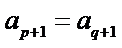

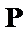
28.若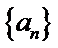
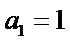
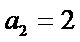
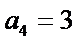
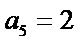
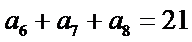
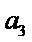
29.若无穷数列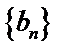
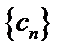
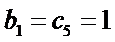
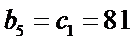
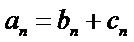
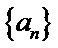
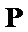
30.设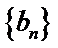
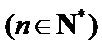
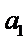
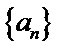
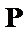
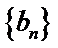
正确答案
解析
由题意知
∴
∴
∴
∴
∴
考查方向
解题思路
反复利用性质求解
易错点
对新定义的性质的不理解;
正确答案
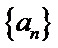
解析
设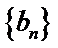
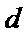
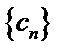
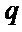
∴
∴
∴
∴
∴
∵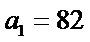
而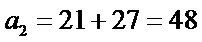
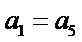
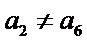
故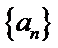
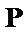
考查方向
解题思路
通过计算,寻找不符合性质的情形“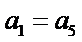
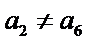
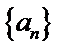
易错点
寻找不到反例
正确答案

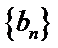
解析
充分性:若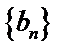
则
若存在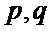
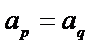
则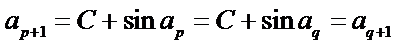
故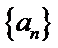
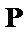
必要性:若对任意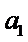
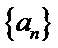
则
设函数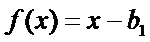
由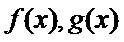
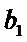
∴一定能找到一个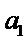
∴
∴
故
∴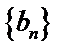
考查方向
解题思路
从充分性和必要性两方面入手证明.
易错点
充要条件的证明.