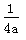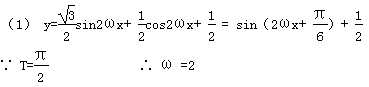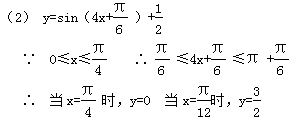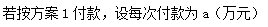理科数学吉林市2011年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

4．已知当x∈R时，函数y=f（x）满足且f（1）=1，则f（100）的值为（）

C34

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的判断与证明等差数列的前n项和及其最值数列与函数的综合

题型：单选题

分值: 5分

5．在三棱柱ABC—A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C 的中心，则AD与平面BB1C1C 所成角的大小是（）

A30O

B45O

C60O

D90O

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面垂直的判定与性质线面角和二面角的求法

题型：单选题

分值: 5分

6．已知球的表面积为20，球面上有A、B、C三点，如果AB=AC=2，BC=2，则球心到平面ABC的距离为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

与球体有关的内切、外接问题

题型：单选题

分值: 5分

1．已知M={|=（1,2）+（3,4），∈R}，N={|=（-2,-2）+μ（4,5），μ∈R}，则

MN=（）

A{（1,1）}

B{（1,1）,（-2,-2）}

C{（-2,-2）}

DΦ

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算相等向量与相反向量

题型：单选题

分值: 5分

2．等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的乘除运算

题型：单选题

分值: 5分

3．已知f（x）=sin（x+），g（x）=cos（x-），则下列结论中正确的是（）

A函数y=f（x）·g（x）的最大值为1

B函数y=f（x）·g（x）的对称中心是（,0），∈Z

C当x∈[-,]时，函数y=f（x）·g（x）单调递增

D将f（x）的图象向右平移单位后得g（x）的图象

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用三角函数的最值

题型：单选题

分值: 5分

7．在样本的频率分布直方图中，共有11个小长方形，若中间一个长方形的面积等于其它10个小长方形面积和的，且样本容量为160，则中间一组的频数为（）

A32

B0.2

C40

D0.25

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

频率分布直方图

题型：单选题

分值: 5分

9．已知有相同两焦点F1、F2的椭圆 + y2=1（m>1）和双曲线 - y2=1（n>0），P是它们的一个交点，则ΔF1PF2的形状是（）

A锐角三角形

B直角三角形

C钝有三角形

D随m、n变化而变化

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质双曲线的几何性质

题型：单选题

分值: 5分

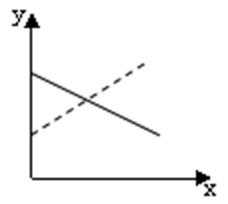
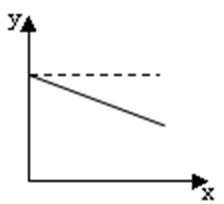
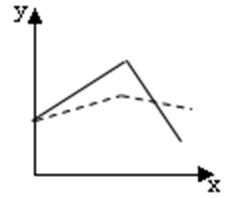
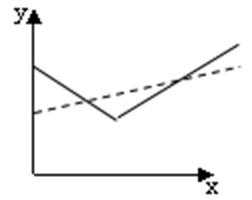
10．在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线y=f（x），另一种是平均价格曲线y=g（x）（如f（2）=3是指开始买卖后二个小时的即时价格为3元；g（2）=3表示二个小时内的平均价格为3元），下图给出的四个图像，其中实线表示y=f（x），虚线表示y=g（x），其中可能正确的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：单选题

分值: 5分

11．直线与抛物线交于两点，过两点向抛物线的准线作垂线，垂足分别为，则梯形的面积为（）

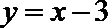
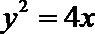
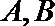
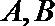
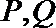
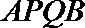
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

题型：单选题

分值: 5分

12．有四根长都为2的直铁条，若再选两根长都为a的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则a的取值范围是（）

A（0,）

B（1,）

C（0,）

D（,）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱锥的结构特征

题型：单选题

分值: 5分

8．函数y=x3-2ax+a在（0,1）内有极小值，则实数a的取值范围是（）

A（0,3）

B（-∞,3）

C（0,+∞）

D（0,）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

16．在平行六面体的一个面所在的平面内，任意画一条直线，则与它异面的平行六面体的棱的条数可能是____________（填上所有可能结果）。

正确答案

4或6或7或8

解析

解析已在路上飞奔，马上就到！

知识点

异面直线的判定排列、组合及简单计数问题

题型：填空题

分值: 4分

13．抛物线y=ax2（a≠0）的准线方程为__________________．

正确答案

y=-

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用抛物线的标准方程和几何性质

题型：填空题

分值: 4分

14．对于任意一个非零实数，它的倒数的倒数是它的本身。也就是说，连续施行两次倒数变换后又回到施行变换前的对象，我们把这样的变换称为回归变换。在中学数学范围内写出这样的变换（写对一个变换给2分，最多得4分）（）

正确答案

相反数的相反数是它本身，集合A的补集的补集是它本身，一个复数的共轭的共轭是它本身，等等.

解析

解析已在路上飞奔，马上就到！

知识点

类比推理

题型：填空题

分值: 4分

15．已知x>0，由不等式≥2·=2，=≥=3,

…，启发我们可以得出推广结论：≥n+1 （n∈N*），则a=_______________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

归纳推理

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

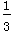
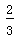
18．质点A位于数轴x=0处，质点B位于x=2处．这两个质点每隔1秒钟都向左或向右平移一个单位，设向左移动的概率为，向右移动的概率为.

（1）求3秒后，质点A在点x=1处的概率；

（2）求2秒后，质点A、B同时在x=2处的概率。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相互独立事件的概率乘法公式

题型：简答题

分值: 12分

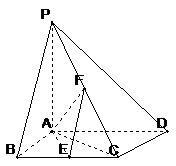
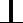
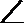
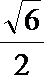
19．如图，已知四棱锥P—ABCD，底面ABCD为菱形，PA平面ABCD，ABC=60O，E，F分别是BC，PC的中点。H为PD上的动点，EH与平面PAD所成最大角的正切值为。

（1）证明：AE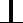PD；

（2）求异面直线PB与AC所成的角的余弦值；

（3）若AB=2，求三棱锥P—AEF的体积。

正确答案

（1）略

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积异面直线及其所成的角直线与平面垂直的判定与性质线面角和二面角的求法

题型：简答题

分值: 12分

17．已知函数y=sinωx•cosωx（ω>0）（ω>0）的周期为 ,

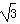
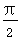
（1）求ω 的值；

（2）当0≤x≤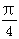 时，求函数的最大值和最小值及相应的x的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用三角函数的最值

题型：简答题

分值: 12分

20．某汽车销售公司为促销采取了较灵活的付款方式，对购买10万元一辆的轿车在一年内将款全部付清的前提下，可以选择以下两种分期付款方案购车：

方案1：分3次付清，购买后4个月第一次付款，再过4个月第二次付款，再过4个月第三次付款．

方案2：分12次付清，购买后1个月第一次付款，再过1个月第二次付款，……购买后12个月第十二次付款。

现规定分期付款中，每期付款额相同，月利率为0.8%，每月利息按复利计息，试比较以上两种方案的哪一种方案付款总数较少？（参考数据：1.0083=1.024，1.0084=1.033，1.00811=1.092，1.00812=1.1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数模型的选择与应用等比数列的基本运算

题型：简答题

分值: 12分

21．已知动点分别在轴、轴上，且满足，点在线段上，且（是不为零的常数）。设点的轨迹为曲线。

（1）求点的轨迹方程；

（2）若，点是上关于原点对称的两个动点（不在坐标轴上），点，求的面积的最大值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量数乘的运算及其几何意义直接法求轨迹方程圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：简答题

分值: 14分

22．已知数列{an}的前n项和，且=1，.

（I）求数列{an}的通项公式；

（II）已知定理：“若函数f（x）在区间D上是凹函数，x>y（x,y∈D），且f’（x）存在，则有< f’（x）”．若且函数y=xn+1在（0,+∞）上是凹函数，试判断bn与bn+1的大小；

（III）求证：≤bn<2.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an由递推关系式求数列的通项公式数列与函数的综合数列与不等式的综合

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷