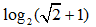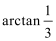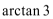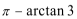- 真题试卷
- 模拟试卷
- 预测试卷
1.若集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.整数




正确答案
{-1,0,1,2,3}
解析
解析已在路上飞奔,马上就到!
知识点
8.将3名同学安排到



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.数列

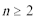
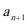


正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
11.定义





正确答案
(1,2009)
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
3.方程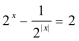
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.对于椭圆
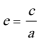
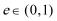
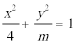
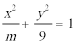

正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
12.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.直线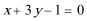
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知二面角






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.高三某班有甲、乙两个学习小组,每组都有10名同学,其中甲组有4名女同学;乙组有6名女同学。现采用分层抽样从甲、乙两组中共抽取4名同学进行学习情况调查。
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的同学中恰有1名女同学的概率;
(3)求抽取的4名同学中恰有2名男同学的概率。
正确答案
(1)乙两组分别抽取
则
即甲、乙两组各抽2人
(2)
(3)甲抽2男,乙抽2女:
甲、乙两组各抽1男1女:
甲抽2女,乙抽2男:
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,圆



(1)求动点M的轨迹C的方程,并说明轨迹是什么图形。
(2)过点B的直线


正确答案
(1)设
则题意
所以
又P在圆
所以

即
轨迹是以

(2)方法一:当直线

设直线

代入椭圆方程得:
△
设
则
由
所以
由(*)、(**)解得

所以
即所求直线方程为:
方法二:设
由
又
所以
因

所以
解得:
若
则
所以直线
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若函数


(2)当



(3)对于函数








正确答案
(1) 当
设

由

则
由
知
所以
(2)当


即
因为



所以


则
(3)因为

设


①若
当


则
所以方程

即


即
当


则

所以
②若
当


所以

所以
当

所以
所以方程

即

所以
即
综上知:




即:

解析
解析已在路上飞奔,马上就到!
知识点
18.如图:圆锥的顶点是S,底面中心为O。OC是与底面直径AB垂直的一条半径,D是母线SC的中点。
(1)求证:BC与SA不可能垂直;
(2)设圆锥的高为4,异面直线AD与BC所成角为
正确答案
(1)证法一:反证法:若
连AC,由AB是直径
则

则
又圆锥的母线长相等,

则
与
所以
证法二:建立坐标系,设圆锥的高为
半径为

所以
(2)建立坐标系,
设底面半径为
由高为4。
则

由AD与BC所成角为
所以
解得
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)记


(2)求
(3)当


正确答案
(1)由
得
即
又
所以

所以

(2)由

=
当
当
(3)由
知
=
因为
所以
则
又
所以
解析
解析已在路上飞奔,马上就到!