- 真题试卷
- 模拟试卷
- 预测试卷
7. 已知函数
如右图所示,如果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 对于非空集合A、B,定义运算





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知幂函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,角





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设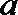
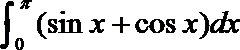
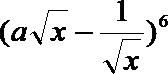
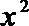
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知定义域为




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 甲、乙两班参加数学知识竞赛,每班出3人组成代表队,每人一道必答题,答对为本队得1分,答错或不答得0分,假如甲队每人答对的概率均为




(Ⅰ)求随机变量

(Ⅱ)用A表示事件“甲、乙两队得分和为3”,B表示事件“甲队得分大于乙队得分”,求P(AB)
正确答案
解:(Ⅰ)
而P(






因而

(Ⅱ)P(AB)=
解析
解析已在路上飞奔,马上就到!
知识点
19.某工厂生产某种产品,每日的成本C(单位:元)与日产里



已知每日的利润


(Ⅰ)求
(Ⅱ)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
解:(Ⅰ)由题意可得:
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数
(Ⅰ)求函数

(Ⅱ)设

正确答案
综上,


法二:
令
因为
所以,当

综上,


(Ⅱ)
由
即函数
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
(Ⅰ)求函数

(Ⅱ)求

正确答案
解:(Ⅰ)
(Ⅱ)
所以,
解析
解析已在路上飞奔,马上就到!
知识点
20.
正确答案
(Ⅰ)证明:
因为


所以函数

(Ⅱ)由题意
则
令

由于


由①得
由于



当

所以在区间



当




综上,函数


又已知



即




所以

解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数

(Ⅰ)当

(Ⅱ)若函数


(Ⅲ) 当




正确答案
解: (Ⅰ)f(x)= x2- lnx+x (
f’(x)=x - + 1==0
∴x1=,x2=
∵(0,

∴f(x)在x= 时取极小值
(Ⅱ)法一:f’(x)=
令g(x)=x2-2ax+ a2+ a, △=4a2-3a2-2a=a2-2a,设g (x)=0的两根
① 当△≤0时 即0≤a≤2,f’(x)≥0
∴f(x)单调递增,满足题意
②当△>0时 即a<0或a>2时
(1)若



f’(x)=x+ -2a ,f’’(x)=1- ≥0
∴f’(x) 在(0,+∞)单调增,不合题意
(2)若

(3) 若

∴f(x)在(0,x1)单调增,(x1,x2)单调减,(x2,+∞)单调增,不合题意
综上得a≤- 或0≤a≤2.
法二:f’(x)=
令g(x)=x2-2ax+ a2+ a, △=4a2-3a2-2a=a2-2a,设g(x)=0的两根
①当△≤0时 即0≤a≤2,f’(x)≥0
∴f(x)单调递增,满足题意
(Ⅲ) g(x)=-lnx-ax2+x,g(x)=--2ax+1=-.
令g((x)=0,即2ax2-x+1=0,当0<a<时,Δ=1-8a>0,所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,不妨设x1<x2,则当x∈(0,x1)∪(x2,+∞)时,g(x)<0,当x∈(x1,x2)时,g(x)>0,
所以,g(x)有极小值点x1和极大值点x2,且x1+x2=,x1x2=.
g(x1)+g(x2)=-lnx1-ax+x1-lnx2-ax+x2
=-(lnx1+lnx2)-(x1-1)-(x2-1)+(x1+x2)
=-ln(x1x2)+(x1+x2)+1=ln(2a)++1.
令h(a)=ln(2a)++1,a∈(0,],
则当a∈(0,)时,h(a)=-=<0,h(a)在(0,)单调递减,
所以h(a)>h()=3-2ln2,即g(x1)+g(x2)>3-2ln2.
解析
解析已在路上飞奔,马上就到!