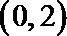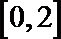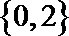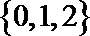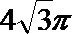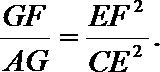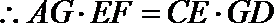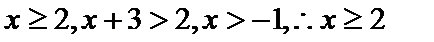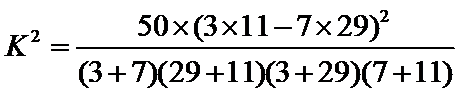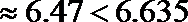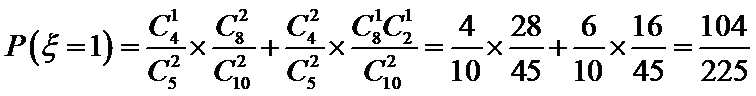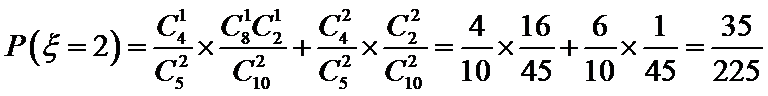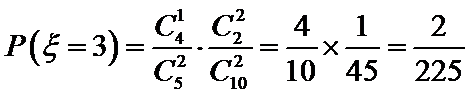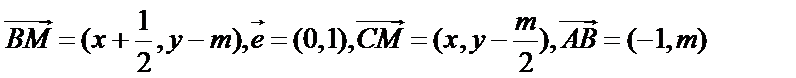- 真题试卷
- 模拟试卷
- 预测试卷
6. 利用如图所示的程序框图在直角坐标平面上打印一系列的点,则打印的点落在坐标轴上的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合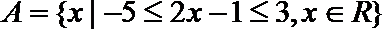
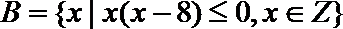
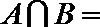
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如果复数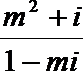
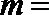
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 如图,设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.焦点为(0,6)且与双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 如图,正方体


为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.直线
正确答案
—15
解析
解析已在路上飞奔,马上就到!
知识点
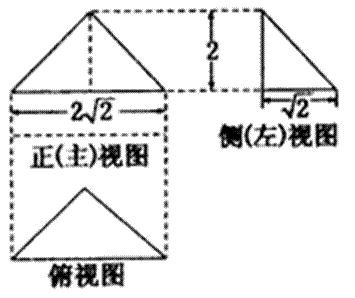
14.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为_______________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两名同学至少有一人参加,且若甲、乙同时参加,则他们发言时不能相邻,那么不同的发言顺序的种数为__________.
正确答案
600
解析
解析已在路上飞奔,马上就到!
知识点
16.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在




(1)求角A的大小;
(2)若

正确答案
(1)

(2)∵
∴
即





解析
解析已在路上飞奔,马上就到!
知识点
19.如图,几何体














(Ⅰ)求证:
(Ⅱ)求二面角
正确答案
(I)
连接




因为



又面

所以四边形
因为



所以
所以
(II)取




以

则
所以
设面

则

令
设面

则

令
则

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分.
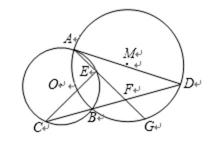
22. 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O、BD于点E、F连结CE.
(1)求证: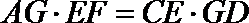
(2)求证:
23. 在直角坐标系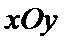
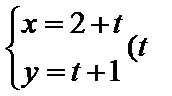

(Ⅰ)求曲线C的普通方程和曲线P的直角坐标方程;
(Ⅱ)设曲线C和曲线P的交点为A、B,求|AB|.
24. 设函数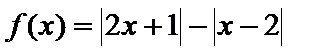
(Ⅰ)求不等式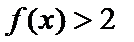
(Ⅱ)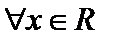
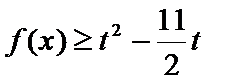
正确答案
22.(1)连结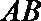
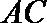
∵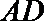
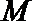
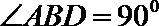
∴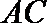
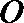
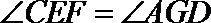
∵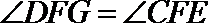
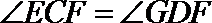
∵
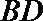
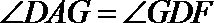
∵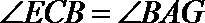
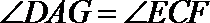
∴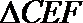
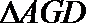
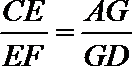
(2)由(1)知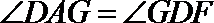
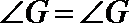
∴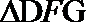
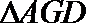
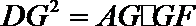
由(1)知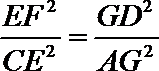
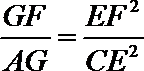
23.(Ⅰ)曲线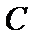
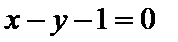
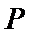
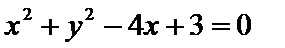
(Ⅱ)曲线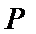
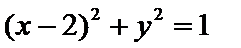
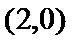
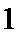
则圆心到直线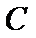
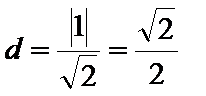
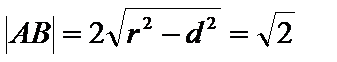
24.
(1)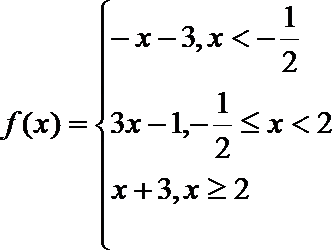
当
当
当
综上所述
(2)易得
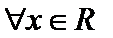
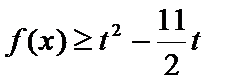
则只需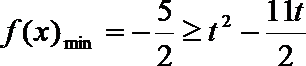
解析
解析已在路上飞奔,马上就到!
知识点
18.现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对 “楼市限购令”赞成人数如下表.
(Ⅰ)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
(Ⅱ)若对月收入在[15,25) ,[25,35)的被调查人中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 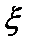
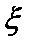
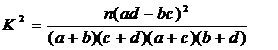
正确答案
(I)先列出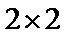
然后利用公式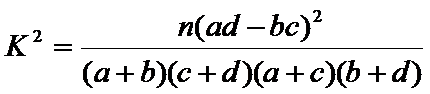
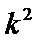
(II)先确定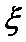
(Ⅰ)2乘2列联表
所以没有99%的把握认为月收入以5500为分界点对“楼市限购令”的态度有差异.
(Ⅱ)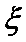
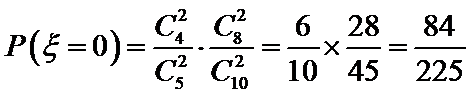
所以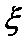
所以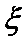
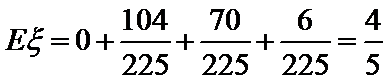
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)当


(2)如果函数












正确答案
(1)当


对于


∴

(2)在区间(1,+∞)上,函数

则
令

且


∵
1) 若



当



此时

并且在该区间上有

当


有

2) 若


从而
要使

所以
又因为h/(x)= –x+2a–

h(x)在(1, +∞)上为减函数,
h(x)<h(1)= 

所以a



解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系中,已知点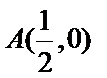
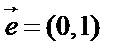
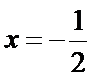

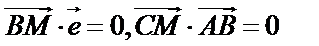
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在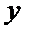
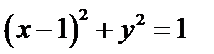
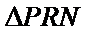
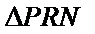
正确答案
(1)设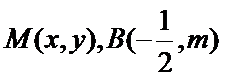
则
由
得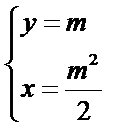
所以动点M的轨迹E的方程为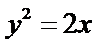
(2)设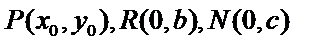
且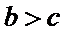
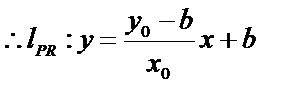
即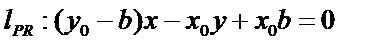
由相切得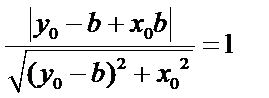
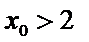
化简得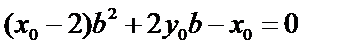
同理得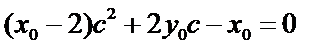
所以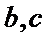
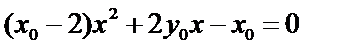
所以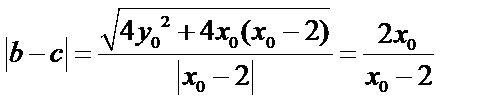
有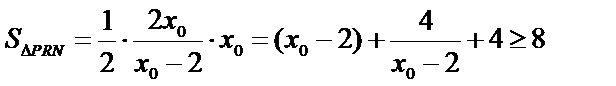
当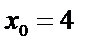
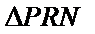
解析
解析已在路上飞奔,马上就到!