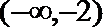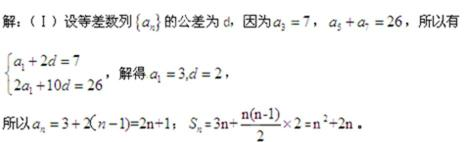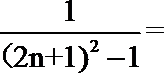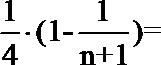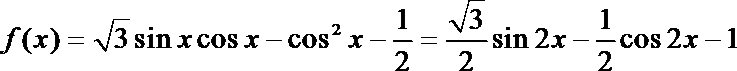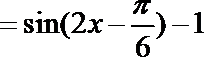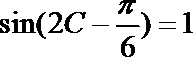- 真题试卷
- 模拟试卷
- 预测试卷
1. 设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 以下有关命题的说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知非零向量a,b满足|a + b| =|a–b |=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 定义在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知二次函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 当x∈(-2,-1)时,不等式(x+1)2<loga|x|恒成立,则实数a的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知函数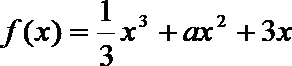
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图,在平行四边形ABCD中 ,AP⊥BD,垂足为P,


正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知在平面直角坐标系中,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 若函数y=
正确答案
1<a<2
解析
解析已在路上飞奔,马上就到!
知识点
20.已知点O为
(1)若

(2)若

正确答案
(1)
(2)解法一:取AB中点为D,AC中点为E。
则
解法二:

解析
解析已在路上飞奔,马上就到!
知识点
18.已知等差数
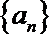
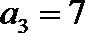
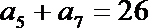
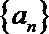
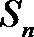
(Ⅰ)求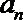
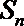
(Ⅱ)令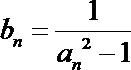
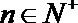
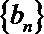
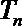
正确答案
(Ⅱ)由(Ⅰ)知
所以bn=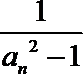
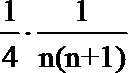
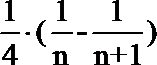
所以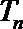
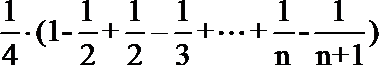
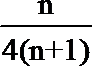
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)讨论
(2)若

(3)设函数





正确答案
(1)


①当



②当




故



(2)


因为

而


(3)当

由

当



所以在
而“


“



而

所以有
所以实数
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知



(1)当

(2)证明:函数

(3)在(1)的条件下,设函数




正确答案
(1)
(2)
∵

即是方程
∵当
∴
∴
∴函数

(3)由题意知:g(x)的值域是f(x)值域的子集。
由(1)知,f(x)的值域是

显然
∴欲使g(x)的值域是f(x)值域的子集
只需
解得:
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数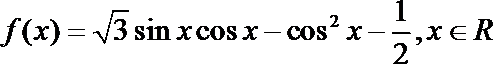
(1) 求函数
(2)已知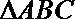
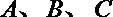
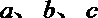
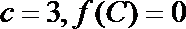
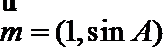
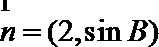
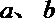
正确答案
(1)
∴ 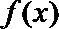
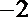


(2)∵ 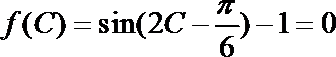
∵ 
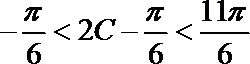

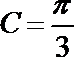
∵ 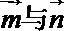
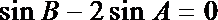
由正弦定理 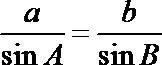
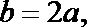
∵ 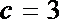
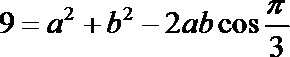
解方程组①②,得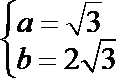
解析
解析已在路上飞奔,马上就到!