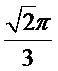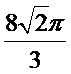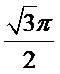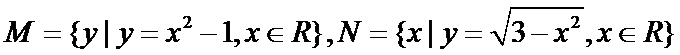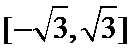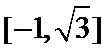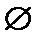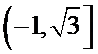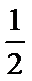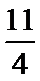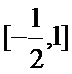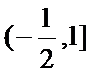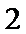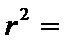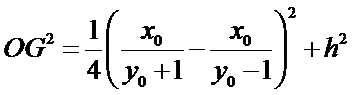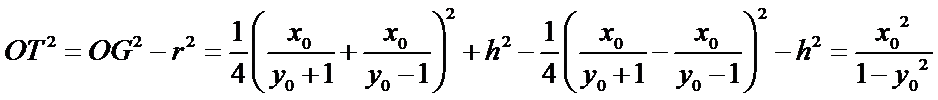- 真题试卷
- 模拟试卷
- 预测试卷
利用一个球体毛坯切削后得到一个四棱锥P—ABCD,其中底面四边形ABCD是边长为1的正方形,PA=1,且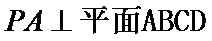
正确答案
解析
由题设知,当所求的球恰为四棱锥的外接球时,球体毛坯体积达到最小值,而此外接球可以与棱长为1的正方体的外接球相同,即
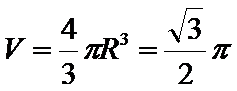
考查方向
解题思路
由题设当所求的球恰为四棱锥的外接球时,球体毛坯体积达到最小值,而此外接球可以转化棱长为1的正方体的外接球,进而求出半径,再求出球的体积。
易错点
1、无法把问题转化为求四棱锥的外接球进而思路受阻;
2、不会分析如何求外接球的半径。
知识点
已知

正确答案
解析
由题设分别画出
而函数


考查方向
解题思路
1、由题设分别画出


易错点
1、解题方法选择不对导致出错。2、在处理

知识点
设集合
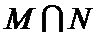
正确答案
解析
由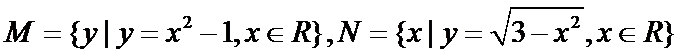
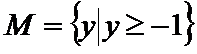
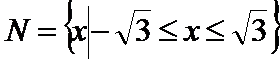
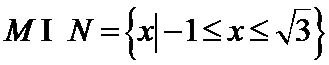
考查方向
解题思路
1、由对数运算解出集合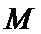
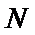
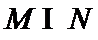
易错点
1、本题易在集合的交并补运算上出问题。 2、对集合的意义理解不到位导致出错。
知识点
已知i是虚数单位,则
正确答案
解析
由

考查方向
解题思路
直接由复数运算求出由
易错点
本题易在复数运算上出错。
知识点
设函数


正确答案
解析
由







考查方向
解题思路
由






易错点
本题易在数列求和运算上出错。
知识点
已知平面向量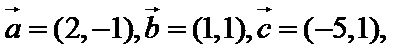
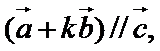
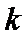
正确答案
解析
由

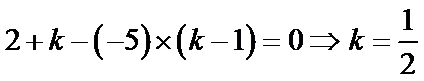
考查方向
解题思路
由
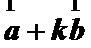
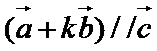
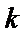

易错点
本题易在坐标运算上出错。
知识点
若

正确答案
解析
由
两边同时除以




考查方向
解题思路
1、由


易错点
1、本题易在对数运算上卡住,难以得到
知识点
下列叙述中正确的是( )
正确答案
考查方向
易错点
1、本题易在充分必要的判断上出问题;
知识点
△ABC中,已知cosA=

正确答案
解析
由




考查方向
解题思路
由



易错点
1、内角和定理的单和互化上符号出错2、易在
知识点
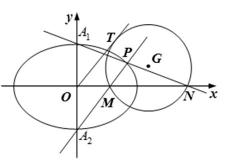
设抛物线









正确答案
解析
如图,由









考查方向
解题思路
1、由直线







易错点
本题难在定义的应用和几何关系的寻找。
知识点
若定义在R上的减函数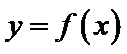
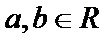
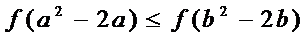
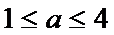
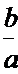
正确答案
解析
由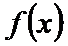
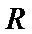
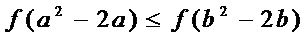
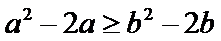
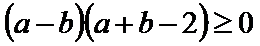
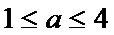
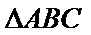
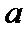
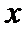
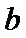
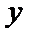
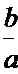
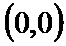
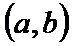
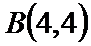
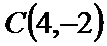
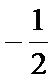
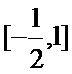
考查方向
解题思路
由函数的单调性结合不等式得出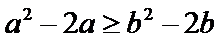
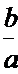
易错点
本题易在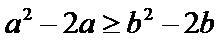
知识点
甲、乙两位同学各拿出六张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( )
正确答案
解析
由解题思路可知,我们来分析接下来两局的情况:①接下来一局若出现奇数(概率为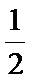
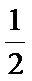
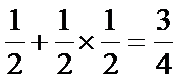
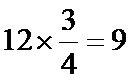
考查方向
解题思路
由题设每局甲、乙两位得1分的概率相同均为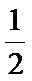
易错点
解题思路不好寻找导致无法解出此题。
知识点
执行程序框图,如果输入

正确答案
4
考查方向
解题思路
本题主要考查了程序框图解题步骤如下:
易错点
本题易在算法的中间运算中出问题。
知识点
已知双曲线C的离心率为2,左、右焦点为


正确答案
考查方向
解题思路
本题主要考查了双曲线的定义和解三角形,解题步骤如下:
易错点
本题易在运算上出问题。
知识点
在△ABC中,a、b、c分别是∠A、∠B、∠C的对边长,已知a、b、c成等比数列,且a2-c2=ac-bc,求∠A的大小及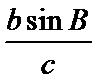
正确答案
∠A=60°;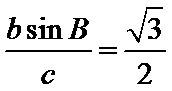
考查方向
易错点
1、对a、b、c成等比结合a2-c2=ac-bc的化简方向的选择
知识点
数列{



正确答案
考查方向
解题思路
本题主要考查了数列中已知递推关系求通项问题,解题步骤如下:
易错点
本题易在运算上和不知如何处理
知识点
设
则
正确答案
128
考查方向
解题思路
本题主要考查了二项式定理和赋值思想,在近几年的各省高考题出现的频率较高二项式展开式的特定项、和赋值思想。解题步骤如下:
易错点
对式子结构的观察不到位。
某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
18.求
19.求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50个的概率;
正确答案



解析
解:由频率分布直方图,得:



考查方向
解题思路
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:由频率算出频率/组距的值再作出对应的图。
易错点
审题不清和考虑不全面导致出错。
正确答案
0.108
∴EX=3×0.6=1.8
解析
解:设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,B表示事件“在未来连续3天里有连续2天日销售量高于10
故所求概率:P(B)=0.6×0.6×0.15×2=0.108.
20.用X表示在未来3天里日销售量高于100个的天数,求随机变量X的分布列和数学期望.
解:依题意,X的可能取值为0,1,2,3,且X~B(3,0.6).
P(X=0)=
P(X=2)=
∴X的分布列为
∴EX=3×0.6=1.8.
考查方向
解题思路
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:
根据题设求出相应概率。
本题主要考查了统计、独立事件的概率及二项分布的应用,解题步骤如下:分析
易错点
审题不清和考虑不全面导致出错。
审题不清和考虑不全面导致出错。
已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
是否不论点E在何位置,都有BD⊥AE?证明你的结论;
若
正确答案
略(具体过程看解析);
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,由线面垂直去证明线线垂直; 不论点E在何位置,都有BD⊥AE.
证明如下:由三视图可知,四

∴BD⊥PC.又∵AC∩
都有AE⊂平面PAC.∴不论点E在何位置,都有BD⊥AE.
考查方向
解题思路
本题考查了证明线线垂直,空间向量在立体几何中的应用,解题步骤如下:根据题设应该由线面垂直去证明线线垂直。
易错点
对线线垂直转化为线面垂直的思路受阻;
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,建好空间直角坐标系后,求出各点坐标,再求出法向量再算出夹角(亦可用传统法进行求解)。
解法1:在平面DAE内过点D作DF⊥AE于F,连结BF.
∵AD=AB=1,
∴Rt△ADE≌Rt△ABE,从而△AD
∴∠DFB为





解法2:如图,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系。则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
从而



设平面ADE和平面ABE的法向量分别为

由
由


∴θ=


考查方向
解题思路
本题考查了证明线线垂直,空间向量在立体几何中的应用,解题步骤如下:建系,求出对应两个半平面的法向量,再由法向量的方面确定其夹角与二面角的关系。
易错点
二面角与法向量夹角之间是相等还是互补的判断。
已知椭圆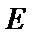
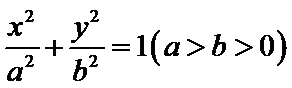
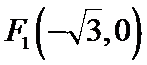
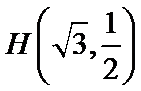
求椭圆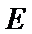
设椭圆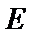
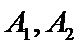
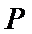
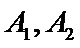
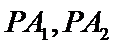
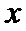
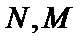
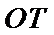
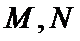
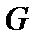
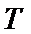
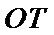
为定值,并求出该定值.
正确答案
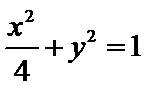
解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,由方程思想求解出标准方程;
解法一:由题意得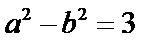
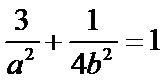
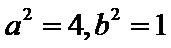
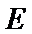
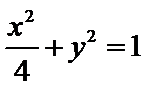
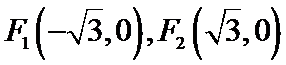
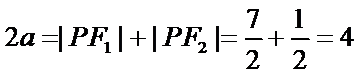
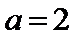

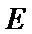

考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和定值问题,解题步骤如下:由方程思想求解出标准方程;
易错点
无法理顺题设的关系导致解题受阻。
正确答案
解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,根据题设求出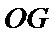
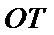
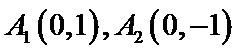
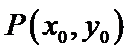
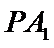
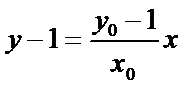
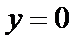
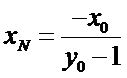
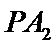
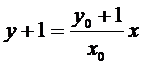
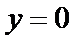
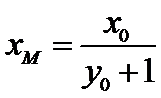
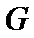
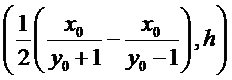
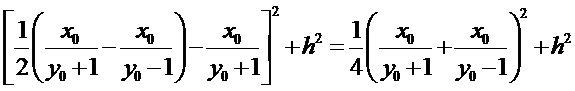
而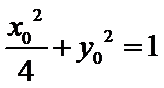

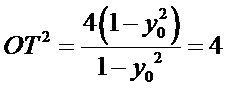
所以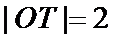
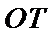
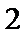
解法二:由(Ⅰ)可知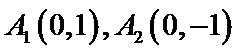
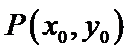
直线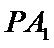
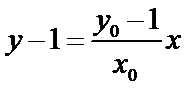
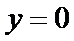
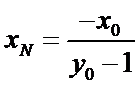
直线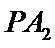
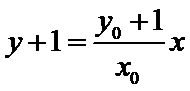
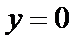
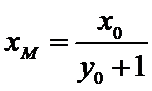
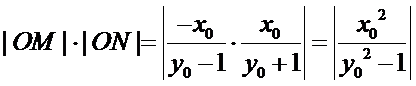
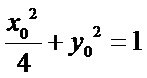
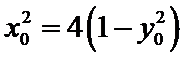
所以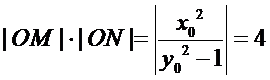

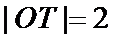
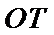
考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和定值问题,解题步骤如下:构建
易错点
无法理顺题设的关系导致解题受阻。
已知函数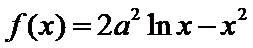

当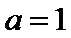
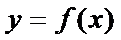
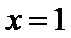
讨论函数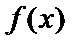
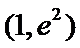

正确答案
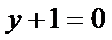
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)求导,然后算出在切点处的导数值,求出切线方程;当 
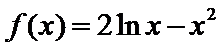
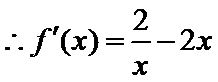
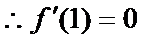
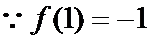
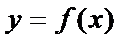
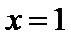
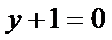
考查方向
解题思路
本题考查导数的应用,解题步骤如下:求导,然后算出在切点处的导数值,求出切线方程。
易错点
忽略函数的定义域导致出错。
正确答案
当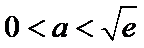
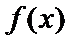
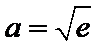
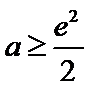
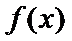
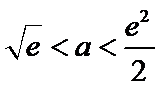
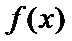
解析
试题分析本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,要注意对参数的讨论。∵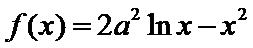
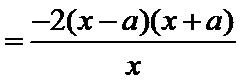
因为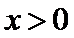
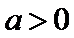

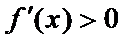
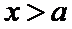
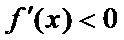
所以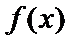
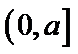
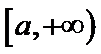
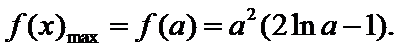
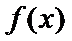
①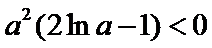
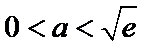

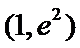
②当
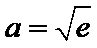
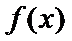
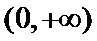
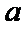
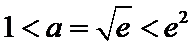
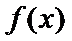
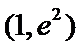
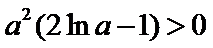
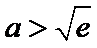

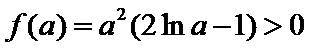
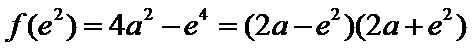

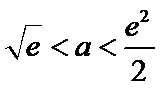

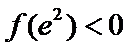
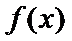
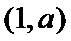
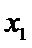
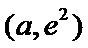
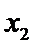
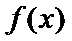
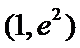
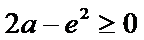
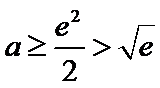
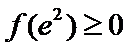
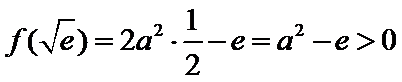

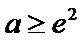
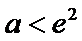
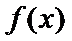
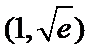
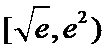
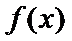
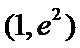
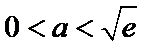
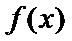
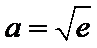

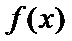
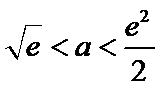
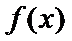
考查方向
解题思路
本题考查导数的应用,解题步骤如下:算出定义域,对参数分类讨论分析单调性,确定最值,再由图确定零点的个数。
易错点
第二问中的易丢对a的分类讨论。
已知AB是圆

求证:MN = MB;
求证:OC⊥MN。
正确答案
详见解题过程;
解析
试题分析:本题属于平面几何的基本问题,由圆的性质直接导出角关系
连结AE,BC,∵AB是圆O的直径,∴∠AEB=90°,∠ACB=90°∵MN=MC,
∴∠MCN=∠MNC又∵∠ENA=∠MNC,∴∠ENA=∠MCN∴∠EAC=∠DCB,
∵∠EAC=∠EBC,∴∠
考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
正确答案
详见解题过程
解析
试题分析:本题属于平面几何的基本问题,由角度等量关系去证所证。
设OC∩BE=F,∵OB=OC,∴∠OBC=∠OCB,由(1)知,∠MBC=∠MCB,∴∠DBM=∠FCM.又∵∠DMB=∠FMC,∴∠MDB=∠MFC,即∠MFC=90°∴OC⊥MN.
考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。