- 真题试卷
- 模拟试卷
- 预测试卷
1. 集合A={﹣1,0,1},B={y|y=cosx,x∈A},则A∩B=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 在△ABC中,a,b,c分别是角A,B,C的对边,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. “
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. (2011•淮南一模)已知点G是△ABC的重心,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 曲线y=e﹣2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 下列四种说法中,错误的个数是( )
①A={0,1}的子集有3个;
②命题“存在

③函数f(x)=e﹣x﹣ex的切线斜率的最大值是﹣2;
④已知函数f(x)满足f(1)=1,且f(x+1)=2f(x),则f(1)+f(2)+…+f(10)=1023.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 等比数列{an}中,a1=2,a8=4,函数f(x)=x(x﹣a1)(x﹣a2)…(x﹣a8),则f′(0)=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 若函数f(x)的导数为f′(x)=﹣x(x+1),则函数f(logax)(0<a<1)的单调减区间为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设f(x)是定义在R上的偶函数,且f(2+x)=f(2﹣x),当x∈[﹣2,0)时,f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数f(x)=
正确答案
a>
解析
解析已在路上飞奔,马上就到!
知识点
16. 函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数.设函数f(x)为定义在[0,1]上的非减函数,且满足以下三个条件:
①f(0)=0;
②f(1﹣x)+f(x)=1x∈[0,1];
③当

则
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知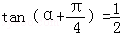
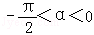
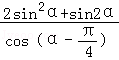
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 在边长为1的正三角形ABC中,设


正确答案
﹣
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知p:对任意m∈[﹣1,1],不等式
正确答案
解:若p成立,由m∈[﹣1,1]得
即a2﹣5a﹣3≥3,解得a≥6或a≤﹣1;
若q成立,则不等式中△>0,解得

若“p或q”为真,“p且q”为假,则命题p与q一真一假,
(1)若p真q假,则
(2)若p假q真,则
综上:a的取值范围是
解析
解析已在路上飞奔,马上就到!
知识点
21. ABC中,a、b、c分别是角A、B、C的对边,


(1)判断△ABC的形状;
(2)若

正确答案
(1)
⇒sinBsinA﹣sinBsin2C=sinAsin2C﹣sinBsin2C
⇒sinB=sin2C,
因为
所以B=π﹣2C⇒B+C=π﹣C⇒π﹣A=π﹣C⇒A=C
即△ABC为等腰三角形.
(2)因为
所以
而
所以
解析
解析已在路上飞奔,马上就到!
知识点
17.在平面直角坐标系xOy中,点A(﹣1,﹣2)、B(2,3)、C(﹣2,﹣1).
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(

正确答案
(1)(方法一)由题设知
则
所以
故所求的两条对角线的长分别为

(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,
则:E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC=

(2)由题设知:

由(

从而5t=﹣11,所以
或者:

解析
解析已在路上飞奔,马上就到!
知识点
19. 设函数
(1)求f(x)的最小正周期;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,
正确答案
(1)


∴周期T=π.
(2)f (A)=2,即
∵a2=b2+c2﹣2bccosA=b2+c2﹣bc,
∴b2+c2﹣bc=3,
又b2+c2+2bc=9,∴bc=2,b+c=3,b>c,解得
解析
解析已在路上飞奔,马上就到!
知识点
22.抛物线y=g(x)过点O(0,0)、A(m,0)与点P(m+1,m+1),其中m>n>0,b<a,设函数f(x)=(x﹣n)g(x)在x=a和x=b处取到极值.
(1)用m,x表示y=g(x)并比较a,b,m,n的大小(要求按从小到大排列);
(2)若
正确答案
(1)由抛物线经过点O(0,0)、A(m,0)
设抛物线方程y=kx(x﹣m)(k≠0),
又抛物线过点P(m+1,m+1),则m+1=k(m+1)(m+1﹣m),得k=1,
所以y=g(x)=x(x﹣m).
∴f(x)=(x﹣n)g(x)=x3﹣(m+n)x2+mnx,
∴f′(x)=3x2﹣2(m+n)x+mn,
∵函数f(x)在x=a和x=b处取到极值,
∴f′(a)=0,f′(b)=0,
∵m>n>0,
∴f′(m)=3m2﹣2(m+n)m+mn=m(m﹣n)>0
f′(n)=3n2﹣2(m+n)n+mn=n(n﹣m)<0,
又b<a,故b<n<a<m.
(2)设切点Q(x0,y0),则切线的斜率k=f′(x0)=3x02﹣2(m+n)x0+mn
又y0=



又切线过原点,故﹣

所以2


两条切线的斜率为k1=f′(0)=mn,
由

∴
所以
又两条切线垂直,故k1k2=﹣1,
所以上式等号成立,有
所以f(x)=x3﹣(m+n)x2+mnx=x3﹣
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数f(x)=x﹣aex﹣1.
(Ⅰ)求函数f(x)单调区间;
(Ⅱ)若f(x)≤0对x∈R恒成立,求a的取值范围。
正确答案
(I)f′(x)=1﹣aex﹣1
当a≤0时,f′(x)>0,f(x)在R上是增函数;
当a>0时,令f′(x)=0得x=1﹣lna
若x<1﹣lna,则f′(x)>0,从而f(x)在区间(﹣∞,1﹣lna)上是增函数;
若x>1﹣lna,,则f′(x)<0,从而f(x)在区间(1﹣lna,+∞)上是减函数。
(II)由(I)可知:当a≤0时,f(x)≤0不恒成立
又当a>0时,f(x)在点x=1﹣lna处取最大值,
且f(1﹣lna)=1﹣lna﹣ae﹣lna=﹣lna
令﹣lna<0得a≥1
故若f(x)≤0对x∈R恒成立,则a的取值范围是[1,+∞)
解析
解析已在路上飞奔,马上就到!