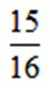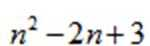- 真题试卷
- 模拟试卷
- 预测试卷
2．如果复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.等差数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．定义行列式运算：
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.一生产过程有4道工序，每道工序需要安排一人照看．现从甲、乙、丙等6名工人中安排4人分别照看一道工序，第一道工序只能从甲、乙两工人中安排1人，第四道工序只能从甲、丙两工人中安排1人，则不同的安排方案共有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.若椭圆经过点P（2，3），且焦点为F1(－2,0),F2(2,0)，则这个椭圆的离心率等于（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7.已知p：关于x的不等式x2+2ax－a>0的解集是R，q：－1<a<0，则p是q 的那么（ ）
A充分非必要条件
B必要非充分
C充要条件
D既非充分又非必要条件
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．现有四个函数：①
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．设集合A＝{x|－1＜x ≤ 2，x∈N}，集合B＝{2，3}，则A∪B等于（ ）
A
B{0，1，2，3}
C{2}
D{－1，0，1，2，3}
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
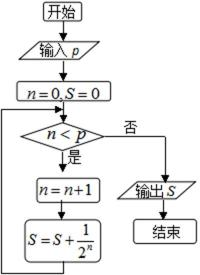
14. 执行下边的程序框图，若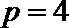
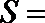
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．如图，一个类似杨辉三角的递推式，则第n行(n≥2)的第2个数为（ ）。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．设变量
正确答案
-8
解析
解析已在路上飞奔，马上就到！
知识点
11.函数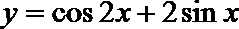
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．若
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
19.已知椭圆
（1）求椭圆方程；
（2）若直线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.甲、乙两名同学参加一项射击游戏，两人约定，其中任何一人每射击一次，击中目标得2分，未击中目标得0分.若甲、乙两名同学射击的命中率分别为
（1）求p的值；
（2）记甲、乙两人各射击一次所得分数之和为ξ，求ξ的分布列和数学期望。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．△ABC中，内角A、B、C所对边分别为a、b、c，已知A＝
（1）求a的长及B的大小；
（2）若0＜x≤B，求函数f(x)＝2sinxcosx＋2cos2x－的值域。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18.如图，在四面体ABCD中，O、E分别是BD、BC的中点，
（1）求证：
（2）求异面直线AB与CD所成角的余弦值；
（3）求点E到平面ACD的距离。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．本题有（1）、（2）、（3）三个选考题，请考生任选2题作答。如果多做，则
（1）矩阵与变换
二阶矩阵
（2）已知圆
①写出此圆的参数方程。
②求圆上一点M到直线
（3）不等式选讲
若不等式
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（1）若
（2）若对任意的
正确答案
解析
解析已在路上飞奔，马上就到！