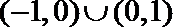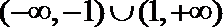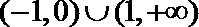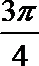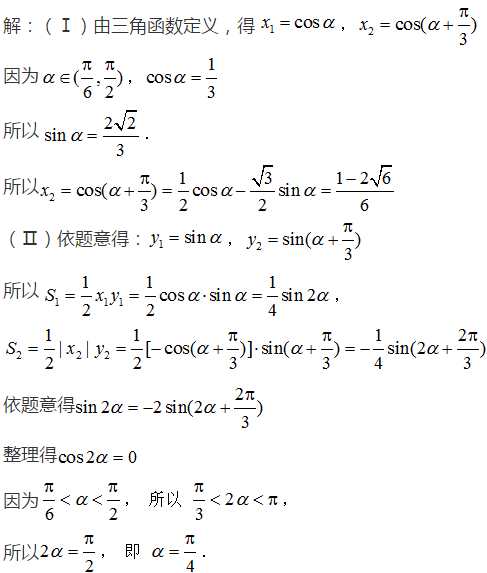- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知锐角



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.对于函数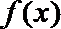

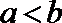
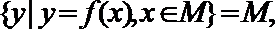

①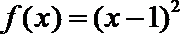
②
③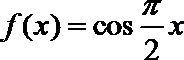
④
其中存在“稳定区间”的函数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若函数

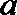
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数
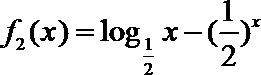
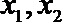
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若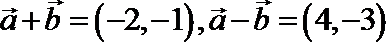
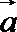
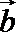
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若复数


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.函数

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.如图,在直角梯形









① 当


② 

③

其中所有正确结论的序号是_________.
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
13.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量



(Ⅰ)当

(Ⅱ)当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(Ⅰ)求c的值;
(Ⅱ)在函数

(Ⅲ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(Ⅰ)若

(Ⅱ)设函数

(Ⅲ)若在区间




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在锐角


(Ⅰ)求
(Ⅱ)若

正确答案
(Ⅰ)由正弦定理可得
因为
所以
在锐角

(Ⅱ)由余弦定理可得
又因为
所以
解得
经检验,由
解析
解析已在路上飞奔,马上就到!
知识点
17.某工厂生产某种产品,每日的成本

已知每日的利润


(Ⅰ)求
(Ⅱ)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在直角坐标系

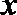
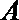
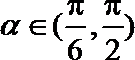
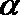
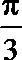
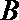
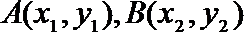
(Ⅰ)若

(Ⅱ)分别过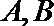


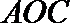
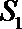
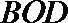
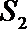


正确答案
解析
解析已在路上飞奔,马上就到!