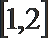- 真题试卷
- 模拟试卷
- 预测试卷
1.已知
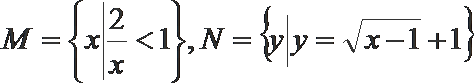
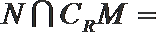
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若等边




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列四个条件中,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.从正方体的棱和各个面的面对角线中选出

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在平面直角坐标系中,有两个区域








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知椭圆:








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在总体中抽取了一个样本,为了便于计算,将样本中的每个数据除以

正确答案
300
解析
解析已在路上飞奔,马上就到!
知识点
14.定义:



正确答案
-6
解析
解析已在路上飞奔,马上就到!
知识点
15.将






正确答案
198
解析
解析已在路上飞奔,马上就到!
知识点
13.已知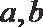
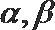
① 若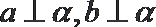
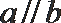
② 若 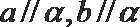
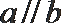
③ 若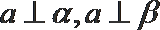
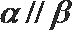
④ 若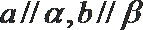
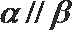
正确命题的个数是( )
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
17.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知







正确答案
18π
解析
解析已在路上飞奔,马上就到!
知识点
19.四枚不同的金属纪念币





(1)求ξ的分布列(用
(2)若恰有一枚纪念币正面向上对应的概率最大,求
正确答案
(1)由题意可得ξ的可能取值为
∴ξ的分布列为
(2)∵

∴
解得
∴

解析
解析已在路上飞奔,马上就到!
知识点
21.如图,椭圆




(1)求椭圆的方程;
(2)设






(I)若

(II)求证:
正确答案
(1)由题设知
由点(1,e)在椭圆上,得
解得

又点


因此,所求椭圆的方程是
(2) 由(1)知




直线

由

故
同理, 
(ⅰ)由①②得

因为


(ⅱ)因为直线


故
从而
因此
又由①②知
所以

解析
解析已在路上飞奔,马上就到!
知识点
20.已知,如图四棱锥













(1)求异面直线

(2)若



正确答案
解法一:(1)
由已知
∴PG=4
如图所示,以G点为原点建立空间直角坐标系o—xyz,则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)
(2)设F(0,y , z)
在平面PGC内过F点作FM⊥GC,M为垂足,则
解法二:
(1)由已知
∴PG=4
在平面ABCD内,过C点作CH//EG交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,
由余弦定理得,cos∠PCH=
(2)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD, ∴GC⊥FM
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG
由GM⊥MD得:GM=GD·cos45°=
解析
解析已在路上飞奔,马上就到!
知识点
18.已知

(1)求函数
(2)若在锐角



正确答案
(1) 

(2) 由(1)及

∵ 
∴ A=60°.
由余弦定理得3=b2+c2-2bccos60°,即(b+c)2=3+bc,
∴ (b+c)2=3+bc≤3+
所以,△ABC周长最大值为
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)若



(2)对于给定的负数


求①


正确答案
(1)易知



由题意得 

(2) ① 由


当 



而


因此,
当




综上得

② 当

当

故当且仅当


解析
解析已在路上飞奔,马上就到!