- 真题试卷
- 模拟试卷
- 预测试卷
2. 函数周期为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知平面向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在《爸爸去哪儿》第二季第四期中,村长给6
①食物投掷地点有远、近两处;
②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;
③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处。
则不同的搜寻方案有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.从0,1,2,3,4,5这六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设向量









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若二项式
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
10.由数字



正确答案
36
解析
解析已在路上飞奔,马上就到!
知识点
13.某学生在参加政、史、地三门课程的学业水平考试中,取得 







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,在四边形





正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14、15题,只能从中选做一题,两题全答的,只计前一题的得分)
14.(参数方程与极坐标)
已知在直角坐标系中曲线









15.(几何证明选讲)
如图,









正确答案
14.
15. 15
解析
解析已在路上飞奔,马上就到!
知识点
18.在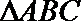
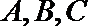
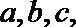
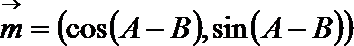

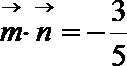
(1)求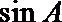
(2)若
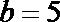
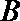


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线



(1)求证:
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图4,在四棱锥










(1)求证:

(2)求证:平面

(3)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某同学用“五点法”画函数
(1)请写出上表的


(2)将







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知一个袋子里有形状一样仅颜色不同的6个小球,其中白球2个,黑球4个. 现从中随机取球,每次只取一球.
(1)若每次取球后都放回袋中,求事件“连续取球四次,至少两次取得白球”的概率;
(2)若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(1)求数列
(2)数列



(3)设各项均不为零的数列






正确答案
解析
解析已在路上飞奔,马上就到!








































