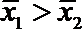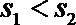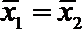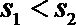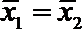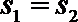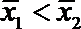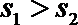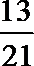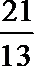- 真题试卷
- 模拟试卷
- 预测试卷
1. 设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
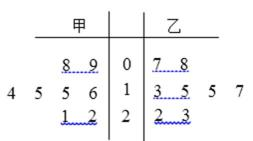
4. 甲乙两名运动员在某项测试中的8次成绩如茎叶图所示,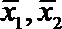
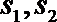
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
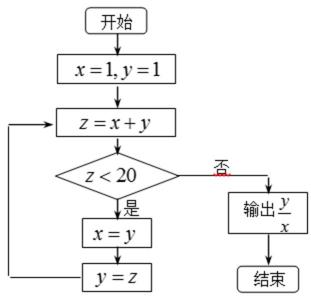
5. 阅读下面的程序框图,运行相应的程序,输出的结果为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 如图,平面











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知区域




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 如图,









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 若



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.极坐标方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 一个数字生成器,生成规则如下:第1次生成一个数












正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13. 已知双曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 对于各项均为整数的数列




不论数列




①

②数列



(1)设数列




(2)试判断数列



(3)对于有限项数列







正确答案
(1)
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
16.在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰. 已知某选手能正确回答第一、二、三、四轮问题的概率分别为



(1)求该选手进入第三轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率;
(3)该选手在选拔过程中回答过的问题的个数记为

正确答案
设事件

由已知
(1)设事件B表示“该选手进入第三轮被淘汰”,
则
(2)设事件C表示“该选手至多进入第三轮考核”,
则
(3)X的可能取值为1,2,3,4



所以,X的分布列为
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数

(1)求函数
(2)讨论

(3)在区间

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

(1)求
(2)求
正确答案
(1)
所以
所以
(2)

因为

所以
又

所以
解析
解析已在路上飞奔,马上就到!
知识点
17. 在四棱锥










(1)求证:

(2)求证:

(3)设





正确答案
(1)取
因为E为PC中点,所以
在梯形

所以

所以

所以
(2)平面




如图,以
则
所以
又由


所以
(3)平面

所以
设平面

所以
所以
所以
注意到

解析
解析已在路上飞奔,马上就到!
知识点
18. 椭圆


(1)求椭圆
(2)过点






正确答案
(1)由已知
又
所以椭圆
(2)根据题意,过点
联立

设

(ⅰ)当
则
因为

所以
(ⅱ)当


此时
又
将①代入②,消去

解得
所以
经检验,所求

解析
解析已在路上飞奔,马上就到!