- 真题试卷
- 模拟试卷
- 预测试卷
5. 高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求两个舞蹈节目不连排,则不同排法的种数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知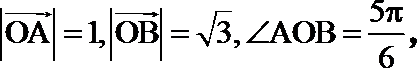
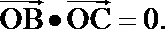
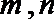
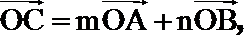
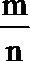
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.点P是双曲线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知命题 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在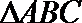
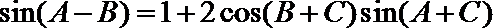
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.能够把圆



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数

①

②存在





若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 6张卡片上分别写有数字1,1,2,3,4,5,从中取4张排成一排,可以组成不同的4位奇数的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知ΔABC中,∠A,∠B,∠C的对边分别为a,b,c,若a = 1, 2cosC + c = 2b,则ΔABC的周长的取值范围是__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,已知球



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.对一个各边不等的凸五边形的各边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色,则不同的染色方法共有________种(用数字作答).
正确答案
30
解析
解析已在路上飞奔,马上就到!
知识点
15.已知定义在




①
②

③函数

④若关于




以上命题中所有正确的命题的序号为_______________.
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
17.在
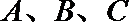
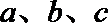
(Ⅰ)求角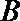
(Ⅱ)若
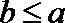

正确答案
解:(1)由已知
得
化简得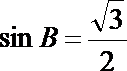
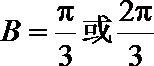
(2)由正弦定理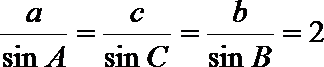

故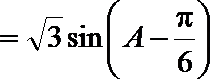
因为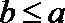
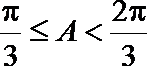
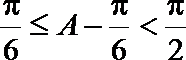
所以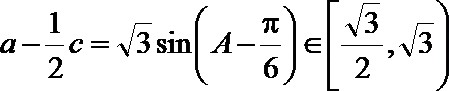
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线










(Ⅰ)求抛物线
(Ⅱ)当


(Ⅲ)若直线



正确答案
解:(1)∵点

∴


(2)法一:∵当



设


∴ 


法二:∵当


∴


∴直线


得



同理可得


(3)法一:设


直线

直线

∴

∴直线



∵



法二:设点


以


⊙

①-②得:直线

当



∵



解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列{an}满足:

(Ⅰ)求
(Ⅱ)记数列{an}前2n项和为


正确答案
解:(I)∵a1=20,a2=7,an+2﹣an=﹣2∴a3=18,a4=5
由题意可得数列{an}奇数项、偶数项分布是以﹣2为公差的等差数列当n为奇数时,


∴an=
(II)s2n=a1+a2+…+a2n=(a1+a3+…+a2n﹣1)(a2+…+a2n
=
结合二次函数的性质可知,当n=7时最大
解析
解析已在路上飞奔,马上就到!
知识点
21. 设

(Ⅰ)当


(Ⅱ)如果存在


(Ⅲ)如果对任意的


正确答案
(Ⅰ)当




所以曲线


(Ⅱ)存在

等价于:


由上表可知:
所以满足条件的最大整数
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答。注意:只能做所选定题目。如果多做,则按所做的第一个题目计分。
22.如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=

(Ⅰ)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.23.设
23.设
(Ⅰ)当

(Ⅱ)当








24.已知曲线




(Ⅰ)写出直线l的普通方程与曲线
(Ⅱ)设曲线






正确答案
22. (Ⅰ)证明:∵AE=

∵在正△ABC中,AD=
∴AD=BE, 又∵AB=BC,∠BAD=∠CBE,
∴△BAD≌△CBE, ∴∠ADB=∠BEC,
即∠ADF+∠AEF=π,所以A,E,F,D四点共圆.
(Ⅱ)解:如图, 取AE的中点G,连接GD,则AG=GE=
∵AE=


∵AD=

∴GD=AG=AD=

所以点G是△AED外接圆的圆心,且圆G的半径为
由于A,E,F,D四点共圆,即A,E,F,D四点共圆G,其半径为
23. (I)


所以解集为
(II)当


由图像知:当


由题意知:


24. 解:(I)

(II)

设


所以当



解析
解析已在路上飞奔,马上就到!
知识点
19. 正方形






(Ⅰ)当点M是EC中点时,求证:BM//平面ADEF;
(Ⅱ)当平面BDM与平面ABF所成锐二面角的余弦值为

正确答案
解:(Ⅰ)以

则



即
(Ⅱ)依题意设

则


则






解析
解析已在路上飞奔,马上就到!