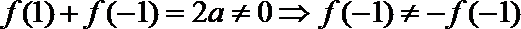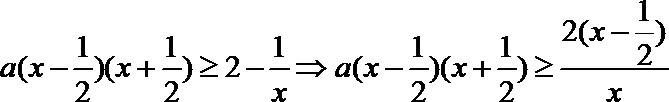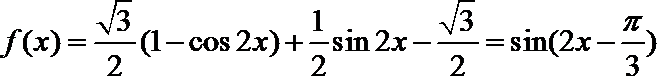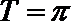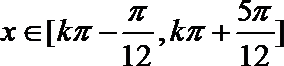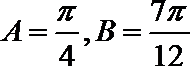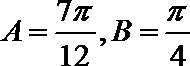- 真题试卷
- 模拟试卷
- 预测试卷
1.已知复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在极坐标系中,







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将圆锥的侧面展开后得到一个半径为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若二项式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某学院的








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.袋中装有同样大小的





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若双曲线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.定义在
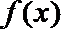
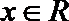
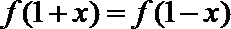
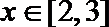
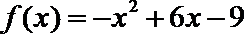
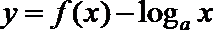
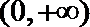
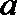
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.某公园草坪上有一扇形小径(如图),扇形半径为















(1)当

(2)函数

(3)若

(4)

其中正确的判断序号是( )(把你认为正确的判断序号都填上)。
正确答案
(2).(3).(4)
解析
解析已在路上飞奔,马上就到!
知识点
2.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数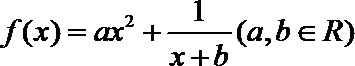
(1)判断函数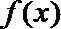
(2)当
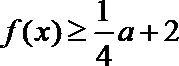
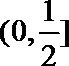
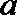
正确答案
(1)函数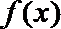
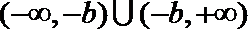
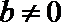
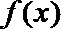
当
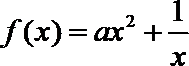
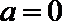
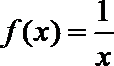
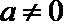
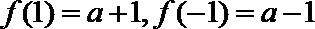
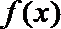
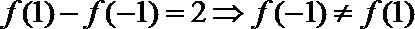
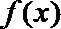
综上知:当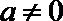
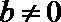
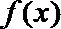
当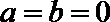
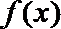
(2)
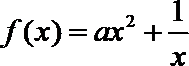
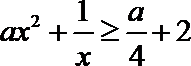
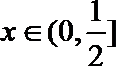
即:
由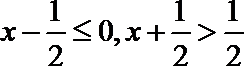
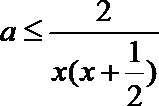
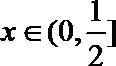
当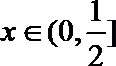
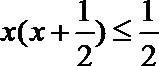

即
解析
解析已在路上飞奔,马上就到!
知识点
21.如图:









(1)设



(2)当


正确答案
(1)由题知:

即


(2)当
因为






在直角三角形







解析
解析已在路上飞奔,马上就到!
知识点
22.抛物线



(1)求抛物线的方程与其准线方程;
(2)直线



①若线段


②求
正确答案
(1)由

圆心

所以抛物线方程为
准线方程为
(2)①设

由


再由
设
则
由题意:
得
得:
所以直线


②

将
化简得:
由(*)得
所以
由于
所以

令







解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数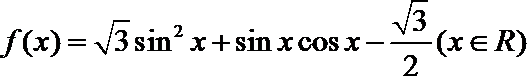
(1)求函数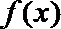
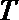
(2)在△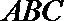
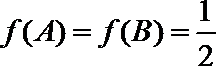
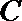
正确答案
(1)
所以周期
由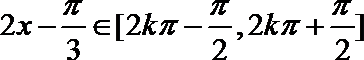
得
即函数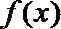
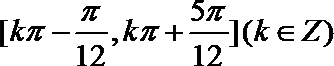
(2)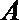
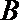
所以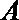
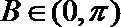
由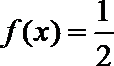
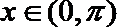
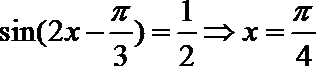
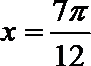
又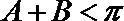
所以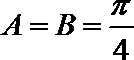
或
所以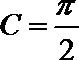
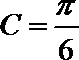
解析
解析已在路上飞奔,马上就到!
知识点
23.若数列








(1)求证:数列
(2)若

(3)设数列



正确答案
(1)因为
所以
所以数列
(2)
当
设
则
当
设
则
因为
所以
即:
解得:
(3)由(2)知

当
当

即:
当

当

若
则
得
所以
综上知,当且仅当

此时
解析
解析已在路上飞奔,马上就到!