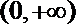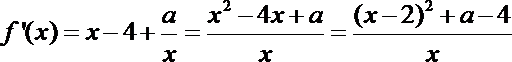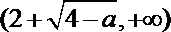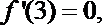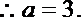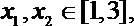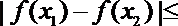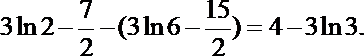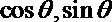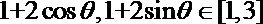- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
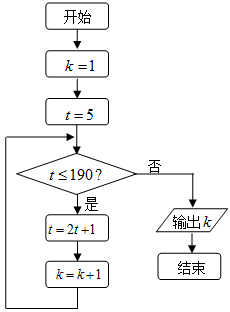
5.如果执行下边的程序框图,那么输出的 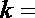
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列四个命题:
①


②命题“若




③从总体中抽取的样本 



④若关于



其中真命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为22的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知定义在R上的函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.己知






正确答案
-20
解析
解析已在路上飞奔,马上就到!
知识点
14.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若随机变量

正确答案
0.1587
解析
解析已在路上飞奔,马上就到!
知识点
12.以直角坐标系的原点为极点,







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知正方体


①以正方体的顶点为顶点的三棱锥的四个面最多只有三个面是直角三角形;
②


③


④



正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
16.在三边互不相等的 

(1)求
(2)求
正确答案
(1)由

由余弦定理得 
即 

(2)


∴
解析
解析已在路上飞奔,马上就到!
知识点
17.某人写了


(1)如果某人写了5封不同的信准备寄给5个人,则他把所有信笺都装错的情况有多少种?
(2)如果某人写了5封不同的信准备寄给5个人,求他随机地把



正确答案
(1))把

(2)根据题意,
∴




∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
18.如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知 
(1)求该几何体的体积;
(2)求二面角
正确答案
(1)



∴
(2)
则


又∵



则



所以二面角

解析
解析已在路上飞奔,马上就到!
知识点
19.动点












(1)当


(2)在(Ⅰ)的条件下,求过
正确答案
(1)依题意知,动点



曲线

∴ 曲线




代人
设
以



(2)由(1)
=
当



解析
解析已在路上飞奔,马上就到!
知识点
20.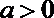
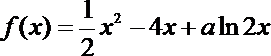
(1)求函数 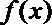
(2)当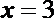
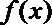
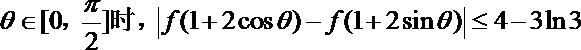
正确答案
(1)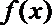
① 当
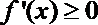
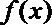
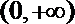
② 当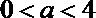
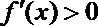
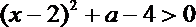
解得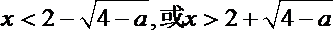
因此,函数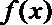
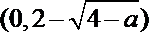
内也单调递增.
令
解得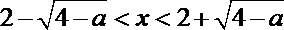
因此,函数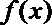
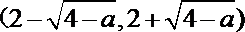
(2)当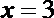
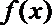

由(1)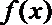
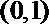
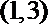
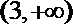
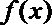
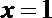
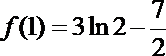
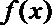
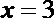

故在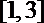
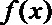
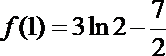

对于任意的
当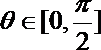
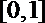
从而
解析
解析已在路上飞奔,马上就到!
知识点
21.已知点



(1)求过



(2)求使不等式


正确答案
(1)
过

下面用数学归纳法证明点 


当

假设

即

根据1),2) 对所有


(2)





设




解析
解析已在路上飞奔,马上就到!