- 真题试卷
- 模拟试卷
- 预测试卷
2.已知命题p:



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若
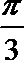
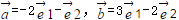
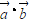
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知各项不为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一个几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将

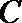
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知集合M={



①M={
②M={
③M={
④M={
其中是“垂直对点集”的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.由直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知

正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
13.已知两条直线

正确答案
-3或1
解析
解析已在路上飞奔,马上就到!
知识点
20.三棱锥









(Ⅰ)求证

(Ⅱ)求证:
(Ⅲ)设


正确答案
证明:(Ⅰ)连结





∴ 



∴ 




∴ 

(Ⅱ)


∴ 
又平面

∴ 

由(Ⅰ)知,

∴ 

连结

又
∴ 

∴
(Ⅲ)由(Ⅰ)(Ⅱ)知,

且

所以分别以

建立空间直角坐标系,如图,
则
∴
设平面

则
令

由(Ⅱ)知

∴ 

∴ 
由图可知,二面角

解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量


(1)求函数
(2)求函数

正确答案
(1)
=
=

图象的对称轴方程为
(2)由于区间

又


最大值
所以函数

解析
解析已在路上飞奔,马上就到!
知识点
18.数列






(1)分别求数列

(2)设

正确答案
(1)由
得
①


(2)因为
所以
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
19.设命题








正确答案
令
因为关于

另一根小于零,所以
即:
解得:命题
因为
所以由不等式
可得:
令
由

故
又不等式

所以命题

因为命题“

(1)若

(2)若


综上可得:

解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆的中心在原点,左焦点

(Ⅰ)求椭圆的标准方程;
(Ⅱ)过




正确答案
(Ⅰ)设椭圆方程为
令

∴椭圆的标准方程为
(Ⅱ)设直线

联立直线与椭圆的方程
得
由题意可知
∴
整理得:
∴
解得
代入
所以直线
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数




(Ⅰ)求函数
(Ⅱ)求实数
(Ⅲ)求证:

正确答案
(Ⅰ)将

∴ 

∴ 
①②联立,解得
∴
(Ⅱ)
∴ 

即

设

∴ 只需证对于任意的
设
1) 当
即

∴


∴
2)当

设

由

题意可知当


∴ 
综上分析,实数
(Ⅲ)令
即

令
∴

∴ 原不等式得证
解析
解析已在路上飞奔,马上就到!