- 真题试卷
- 模拟试卷
- 预测试卷
1.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知条件




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.要从10名男生和5名女生中选出6人组成啦啦队,若按性别依此比例分层抽样且某男生担任队长,则不同的抽样方法数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,两块斜边长相等的直角三角板拼在一起,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知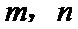
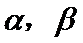
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.类似于十进制中逢10进1,十二进制的进位原则是逢12进1,采用数字0,1,2…,9和字母M、N共12个计数符号,这些符号与十进制数的对应关系如下表:
例如,由于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在一次学科内研究性学习课上,老师给出问题:研究函数

的性质.随机选择5位同学得到的结果如下:
①当

②当

③对于任意的


④对于任意的

⑤当


其中所有正确结果的序号为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设变力






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 

正确答案
-10
解析
解析已在路上飞奔,马上就到!
知识点
12. 如图,已知









正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.在直角坐标系xOy中,直线L的参数方程为


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,在三棱锥















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图








(Ⅰ)若


(Ⅱ)求
正确答案
(I)因为A点的坐标为



(Ⅱ)因为


所以由余弦定理得




解析
解析已在路上飞奔,马上就到!
知识点
17.甲、乙两位同学参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,绘制成茎叶图如下:
(Ⅰ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由;
(Ⅱ)若将频率视为概率,对乙同学在今后的3次数学竞赛成绩进行预测,记这3次成绩中高于80分的次数为


正确答案
由茎叶图知甲乙两同学的成绩分别为:
甲:82 81 79 88 80 乙:85 77 83 80 85
(Ⅰ)派乙参赛比较合适,
理由如下:
甲的平均分

又甲的标准差的平方(即方差)


甲乙平均分相同,但乙的成绩比甲稳定,
(Ⅱ)记乙同学在一次数学竞赛中成绩高于80分为事件


其分布列为:

或直接使用下法:



【注】本题第(Ⅰ)小题的结论唯一但理由不唯一,只要考生从统计学的角度给出其合理解答即可得分.如还可有如下解释:
法2 从统计学的角度看,甲获得






法3 若从学生得


乙获得


乙的平均分

解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列


数列


(Ⅰ)求

(Ⅱ)假设数列




正确答案
(Ⅰ)当
当
所以,
由
所以,

所以,
(Ⅱ)证明:当
当
故
综上,
解析
解析已在路上飞奔,马上就到!
知识点
18.已知四棱锥




(Ⅰ)求证:
(Ⅱ)求二面角
(Ⅲ)线段



正确答案
解法一:
(Ⅰ)因为



因为



在


由根据三垂线定理可得知:
(Ⅱ)设






作


所以

由已知得,

所以

所以二面角

(Ⅲ)当



证明:取




所以


所以

又


解法二:以D为原点,以DA、DC、DP为x轴、y轴、z轴建立空间直角坐标系,
则



(Ⅰ)

所以
所以
(Ⅱ)






设平面



所以


(Ⅲ)令
由已知,



即


所以 当



解析
解析已在路上飞奔,马上就到!
知识点
19.如图,椭圆











(Ⅰ)求椭圆
(Ⅱ)设点





正确答案
(Ⅰ) 由题意知:
解得
∴ 椭圆的方程为
(Ⅱ)假设存在椭圆上的一点
与以




化简整理得:
∵ 点在椭圆上,∴
解得:




∴ 椭圆上存在点


与以

解析
解析已在路上飞奔,马上就到!
知识点
20.设










(Ⅰ)设函数

(i) 求证:函数

(ii)求函数
(Ⅱ) 已知函数









正确答案
(1)(i)由
因为



(ii)当

所以


当


因为
所以当



当




综上所述,当


当


(2)由题设知,







①当



所以由


②当

于是


所以
③当


与题设不符.
因此,综合①②③得所求的
解析
解析已在路上飞奔,马上就到!