- 真题试卷
- 模拟试卷
- 预测试卷
15．设
（Ⅰ）求角
（Ⅱ）设向量
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16.平安汽车租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17. 如图所示，在正方体ABCD－A1B1C1D1中，E是棱DD1的中点．
（Ⅰ）求平面ABCD与平面 A1BE所成二面角的平面角的正弦值；
（Ⅱ）请问：在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20. 已知数列｛an｝为等差数列，且满足an＋1＝an2－nan＋1，n＝1，2，3，…
（Ⅰ）求数列｛an｝的通项公式；
（Ⅱ）求证：
（Ⅲ）当
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19.已知
（Ⅰ）判断函数
（Ⅱ） 求证：
（Ⅲ） 已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18. 设函数
（Ⅰ）若
（Ⅱ）求经过坐标原点
（Ⅲ）令
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知正方形ABCD的对角线AC与BD相交于E点，将
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8.如图所示，函数
Af1（x），f3（x）
Bf2（x）
Cf2（x），f3（x）
Df4（x）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.满足条件M∪{1,2}={1，2，3}的集合M的个数是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.已知函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.如果
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6. 如果函数
A
B－
C1
D－1
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.若一个等差数列前3项和为3，最后3项和为30，且所有项的和为99，则这个数列有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2.若向量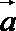
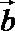
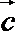
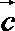
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9. 函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10. 设变量x，y满足则2x＋3y的取值范围是________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11. 命题p：方程x2＋mx＋1＝0有两个不相等的实数根，命题q：方程4x2＋4(m＋2)x＋1＝0没有实数根．若“p且q”为假命题，则实数m的取值范围为_________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12.直线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13. 若正数a，b满足
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14. 已知正三棱柱
正确答案
解析
解析已在路上飞奔，马上就到！