- 真题试卷
- 模拟试卷
- 预测试卷
1.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若全集U=R,集合A={

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
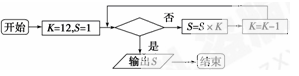
5.程序框图如图,如果上述程序运行的结果S=1320,那么判断框中应填入 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设三条不同的直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.两圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列有关命题的说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.数列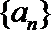
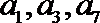
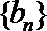
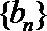
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数
①若
②

③

④

⑤当

其中正确的命题为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知非零向量








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.双曲线
正确答案
13
解析
解析已在路上飞奔,马上就到!
知识点
13.甲、乙等五名志愿者被分配到上海世博会中国馆.英国馆.澳大利亚馆.俄罗斯馆四个不同的岗位服务,每个岗位至少一名志愿者,则甲.乙两人各自独立承担一个岗位工作的分法共有( )种。(用数字做答)
正确答案
72
解析
解析已在路上飞奔,马上就到!
知识点
15.已知一系列函数有如下性质:
函数


函数


函数


………………
利用上述所提供的信息解决问题:
若函数


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.某几何体的三视图,其中正视图是腰长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某学校数学兴趣小组有10名学生,其中有4名女同学;英语兴趣小组有5名学生,其中有3名女学生,现采用分层抽样方法(层内采用不放回简单随机抽样)从数学兴趣小组、英语兴趣小组中共抽取3名学生参加科技节活动。
(1)求从数学兴趣小组、英语兴趣小组各抽取的人数;
(2)求从数学兴趣小组抽取的学生中恰有1名女学生的概率;
(3)记

正确答案
解:(1)抽取数学小组的人数为2人;英语小组的人数为1人;
(2)

(3)


解析
解析已在路上飞奔,马上就到!
知识点
20.已知点








(1)求动点
(2)已知点





正确答案
解:(1)设
则点
∴
又 
∵ 


∴ 点
(2)假设椭圆



且有
又 

∴ 
得
∴ 
∴ 直线MN的方程为
∴ 椭圆上存在点



解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在六面体










(Ⅰ)求证: 

(Ⅱ)求二面角
(Ⅲ) 求五面体
正确答案
解法一 向量法

则A(0,0,2),
B(2,0,2),C(0,1,2),E(2,0,0),
G(0,2,0),F(2,1,0)
(Ⅰ)
∴

故 BF//平面ACGD
(Ⅱ)

则


而平面ADGC的法向量
∴
故二面角D-CG-F的余弦值为
(Ⅲ)设DG的中点为M,连接AM.FM,
则
=



所以MF//DE,且MF=DE又∵AB//DE,且AB=DE
∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1


在直角三角形MNF中,MF=2,MN
∴




故二面角D-CG-F的余弦值为
(Ⅲ)

=

解析
解析已在路上飞奔,马上就到!
知识点
16. A、B是直线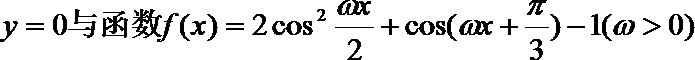
(1)求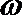
(2)在锐角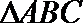
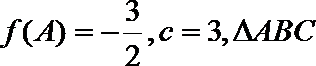
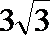
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知三次函数




(1)若曲线



(2)若


正确答案
(1)由导数的几何意义
∴
∴ 
(2)∵ 
∴
由 

∵ 
∴ 当





∴ 
∵ 

∵ 
∴
∴ 

∴ 


解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列

(1)写出

(2)设




正确答案
解:(1)∵
∴
当

∴ 
∴
当

∴数列
(2)
令

当
∴ 

故当
即当
要使对任意的正整数

不等式
则须使
即
∴
∴ 实数
另解:
∴ 数列
∴
解析
解析已在路上飞奔,马上就到!