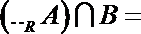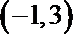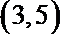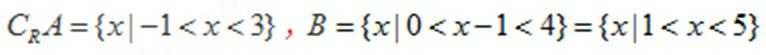• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
  • 教师招募
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
理科数学 黄冈市2016年高三期末试卷
精品
|
立即下载

理科数学 热门试卷

X 查看更多试卷
试卷目录
1、单选题
1
2
3
4
5
6
7
8
9
10
11
12
2、简答题
13
14
15
16
17
18
19
20
21
22
  • 真题试卷
  • 模拟试卷
  • 预测试卷
查看更多 >
单选题 本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。
1
题型： 单选题
|
分值: 5分

3．欧拉公式（为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，表示的复数在复平面中位于

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

B

解析

，对应点为，由于，因此，点在第二象限，故选B．

考查方向

复数的几何意义

解题思路

将欧拉公式转换成对应点的坐标。根据坐标判断。

易错点

阅读理解的能力

知识点

复数代数形式的混合运算
1
题型： 单选题
|
分值: 5分

5．等差数列前项和为，且，则数列的公差为

A

B

C

D

正确答案

B

解析

由得，所以，故选B．

考查方向

考查等差数列前n项和公式

解题思路

根据前n项和公式求公差

易错点

项数和项弄混淆

知识点

等差数列的基本运算等差数列的前n项和及其最值
1
题型： 单选题
|
分值: 5分

7．已知，则

A          

B

C

D

正确答案

C

解析

所以所以，故选C三角函数公式 

考查方向

两角和与差的正弦（余弦）公式

解题思路

找出所求角与已知角的和或者差的关系，然后应用诱导公式把“所求角”变成“已知角”

易错点

角的取值范围弄错导致求值错误。

知识点

三角函数的化简求值两角和与差的正弦函数二倍角的正弦
1
题型： 单选题
|
分值: 5分

8．已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的

体积等于

A

B

C

D

正确答案

C

解析

还原成的几何体如图所示，利用体积计算公式计算，所以选C

考查方向

三视图与几何体的体积

解题思路

利用三视图尺寸还原成立体图形，利用立体图形体积公式求解。

易错点

立体感不强，三视图尺寸理解错误

知识点

简单空间图形的三视图棱柱、棱锥、棱台的体积
1
题型： 单选题
|
分值: 5分

11．若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为

A

B

C

D

正确答案

A

解析

我们应该掌握一些特殊的多面体与外接球的特征．正四面体外接球的球在其高上，且把高分成两部分，正方体，长方体的对角线就是其外接球的直径，正三棱锥，正四棱锥的外接球的球心在其高上，具体计算可借助相应的直角三角形．

考查方向

本题考查多面体及其外接球问题.正四棱锥与外接球

解题思路

找到高和外接球半径的关系，利用基本不等式求解。

易错点

找不到关系和不会利用基本不等式

知识点

棱柱、棱锥、棱台的体积球的体积和表面积与球体有关的内切、外接问题
1
题型： 单选题
|
分值: 5分

12．关于函数，下列说法错误的是

A是的极小值点

B函数有且只有1个零点

C存在正实数，使得恒成立

D对任意两个正实数，且，若，则

正确答案

C

解析

，，

且当时，，函数递减，

当时，，函数递增，

因此是的极小值点，A正确；

，

，

所以当时，恒成立，即单调递减，

又，，

所以有零点且只有一个零点，B正确；

设，

易知当时，，

对任意的正实数，

显然当时，，即，，

所以不成立，C错误；

作为选择题这时可得结论，选C，

下面对D研究，因为，

即，变形为，

设，，代入上式解得，所以，由导数的知识可证明是增函数，

又（洛必达法则），

所以，即 命题的判断

考查方向

函数的性质，知识点多，难度大。

解题思路

根据函数的性质，依次判断每个选项

易错点

对命题理解不透彻，对函数的性质掌握不好

知识点

命题的真假判断与应用导数的运算
1
题型： 单选题
|
分值: 5分

10．如图所示，在正六边形ABCDEF中，点P是△CDE内(包括边界)的一个动点，

设，则的取值范围是

AA．

B

C

D

正确答案

B

解析

这类题型需要建立好坐标系，根据坐标系找可行域更可行  

考查方向

向量在几何中的应用；平面向量的基本定理及其意义

解题思路

先建立直角坐标系，然后求出EC和CD的方程，找到可行域，将平面向量用坐标形式表示，带入可行域中，求得。

易错点

建立坐标系错误、计算能力弱

知识点

平面向量的基本定理及其意义向量在几何中的应用
1
题型： 单选题
|
分值: 5分

4．函数则

A

B

C

D

正确答案

A

解析

故选A

考查方向

分段函数、指数函数对数函数

解题思路

根据题意，层层带入到函数中

易错点

分段函数的函数定义域弄混淆

知识点

函数的值指数幂的运算对数的运算性质
1
题型： 单选题
|
分值: 5分

6．若  ，则的大小关系

A

B

C

D

正确答案

D

解析

，，，所以，故选D．

考查方向

比较大小，定积分．

解题思路

先求定积分，再比较大小。

易错点

定积分求不出来

知识点

定积分的计算不等式的性质
1
题型： 单选题
|
分值: 5分

9．已知函数的周期为，若将其图象沿轴向右平移个单位，所得图象关于原点对称，则实数的最小值为

A

B

C

D

正确答案

D

解析

，由得，即，向右平移个单位后得，其图象关于原点对称，即为奇函数，，，，最小的正数，故选D

考查方向

函数图象的平移，函数的奇偶性

解题思路

先求出平移后的函数，然后根据奇函数的定义化简求参数，最后利用三角函数周期的特点判断最小正周期。

易错点

函数平移概念理解不透彻

知识点

函数y=Asin（ωx+φ）的图象变换二倍角的余弦
1
题型： 单选题
|
分值: 5分

2．命题“若，则”的否命题为

A若，则且

B若，则或

C若，则且

D若，则或

正确答案

D

解析

命题“若，则”的否命题是“若，则或”．故选D．

考查方向

主要考察四种命题、简易逻辑等

解题思路

仔细分析，按照定义求解。

易错点

对四种命题概念混淆，“或”“且”不分

知识点

四种命题及真假判断
1
题型： 单选题
|
分值: 5分

1．已知集合，则

A

B

C

D

正确答案

A

解析

由已知得，,

所以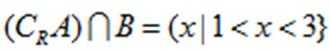，故选A

考查方向

主要考查集合间的基本运算，解不等式以及对数的概念。

解题思路

先解出集合A和集合B，然后利用集合间的基本运算求解

易错点

对对数的概念理解不透彻，不会解不等式

知识点

交、并、补集的混合运算
简答题（综合题） 本大题共90分。简答应写出文字说明、证明过程或演算步骤。
1
题型：简答题
|
分值: 5分

13．已知平面直角坐标系中，，，则向量在向量的方向上的投影是________．

正确答案

解析

向量a在向量b的方向上的投影是，

考查方向

向量的数量积的概念．

解题思路

利用向量的数量积性质求解

易错点

向量的在另一个向量上投影的概念理解有误

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系
1
题型：简答题
|
分值: 5分

14．若函数，为偶函数，则实数_________．

正确答案

解析

由题意，则，即，．

考查方向

函数的奇偶性

解题思路

利用函数奇偶性质求解

易错点

对函数性质理解不透彻

知识点

函数奇偶性的性质
1
题型：简答题
|
分值: 12分

17．在等比数列中，．(Ⅰ)求数列的通项公式；(Ⅱ)设，且为递增数列，若，求证：．

正确答案

（1）时，； 时，

（2）由题意知：

∴

∴

解析

（1）具体的分析如下：时，；时， 

（2）由题意知： 

∴∴

∴

∴  

考查方向

等比数列的通项公式，裂项相消法求和．

解题思路

先求出bn，然后用裂项相消求和

易错点

分类讨论p=1和p不等1时候的情况

知识点

由数列的前几项求通项等比数列的基本运算数列与不等式的综合
1
题型：简答题
|
分值: 12分

19．如图，已知长方形中，，，为的中点．将沿折起，使得平面⊥平面．(Ⅰ)求证：(Ⅱ)若点是线段上的一动点，问点在何位置时，

二面角的余弦值为．

正确答案

（1）证明：

∵长方形ABCD中，AB=，AD=，M为DC的中点，

∴AM=BM=2，∴BM⊥AM.

∵平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，BM⊂平面ABCM

∴BM⊥平面ADM  ∵AD⊂平面ADM   ∴AD⊥BM；

（2）建立如图所示的直角坐标系，设，

则平面AMD的一个法向量， ，

设平面AME的一个法向量为     取y=1，得

所以，

 因为，

求得，所以E为BD的中点．

解析

已知面面垂直，得到线线垂直。建立空间直角坐标系计算求得  

考查方向

面面垂直的性质定理，二面角．

解题思路

求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角.

易错点

计算能力，找二面角的平面角

知识点

平面与平面垂直的判定与性质线面角和二面角的求法
1
题型：简答题
|
分值: 12分

21．已知函数．(Ⅰ)若直线与的反函数的图象相切，求实数k的值；(Ⅱ)设，且试比较三者的大小，并说明理由．

正确答案

(1)的反函数为 设切点为  则切线斜率为故 

（2）不妨设令则所以在上单减，故取则 令则在上单增，故取则综合上述知，

解析

反函数的应用很重要，学会灵活应用举一反三，导数的应用便于解决实际问题，利用导数求曲线的切线，导数与函数的单调性、最值，比较大小。

考查方向

利用导数求曲线的切线，导数与函数的单调性、最值，比较大小

解题思路

的反函数是，问题为求过原点所作曲线的切线的斜率，方法是设切点坐标为，由导数的几何意义可得解；（2）首先不妨设，要比较大小比较方便，只要作差，计算后因式分解可得

易错点

曲线“在点处的切线”与“过点的切线”的区别与联系

知识点

函数单调性的性质反函数导数的几何意义
1
题型：简答题
|
分值: 5分

15．设实数x，y满足约束条件则的最大值为________．

正确答案

10

解析

做出题目约束条件表示的可行域，在可行域内部，作出直线，把直线向上平移到约束条件最大，可得最大值为10.

考查方向

简单的线性规划问题．

解题思路

求目标函数的最大值或最小值,必须先求出准确的可行域,令目标函数等于0,将其对应的直线平行移动,最先通过或最后通过的顶点便是最优解

易错点

可行域求解错误

知识点

其它不等式的解法
1
题型：简答题
|
分值: 5分

16．如图所示，已知中，，，为边上的一点，

为上的一点，且，则________．

正确答案

解析

本题已知直角中的所有量（三边，三角），要求的线段长可能在直角中，此三角形中已知一直角边，要求另一直角边，要么先求得斜边，要么先求得一锐角，再结合已知条件发现锐角与直角中的角有联系，由此得出解法．

考查方向

解三角形．

解题思路

利用解直角三角形相关公式求解

易错点

分析试题，找不到解决问题的突破口。

知识点

解三角形的实际应用
1
题型：简答题
|
分值: 12分

18．如图，中，三个内角、、成等差数列，且(Ⅰ)求的面积；(Ⅱ)已知平面直角坐标系，点,若函数的图象经过、、三点，且、为的图象与轴相邻的两个交点，求的解析式．

正确答案

（1）在△ABC中，

由余弦定理可知：           

 ∴            

 又∵                  

      

 (2)T=2×（10+5）=30,

∴         

 ∵，

，        

，

解析

已知两边一角，三角形可解。利用余弦定理OC.进而确定三角函数式的表达式，得到周期和坐标  

考查方向

 三角形的面积，余弦定理，三角函数的解析式．

解题思路

先解三角形，然后确定三角函数表达式，进而求周期

易错点

解三角形，余弦定理求解错误

知识点

正弦函数的图象函数y=Asin（ωx+φ）的图象变换
1
题型：简答题
|
分值: 12分

20．小明同学制作了一个简易的网球发射器，可用于帮忙练习定点接发球，如图1所示，网球场前半区、后半区总长为23.77米，球网的中间部分高度为0.914米，发射器固定安装在后半区离球网底部8米处中轴线上，发射方向与球网底部所在直线垂直．为计算方便，球场长度和球网中间高度分别按24米和1米计算，发射器和网球大小均忽略不计．如图2所示，以发射器所在位置为坐标原点建立平面直角坐标系，x轴在地平面上的球场中轴线上，y轴垂直于地平面，单位长度为1米．已知若不考虑球网的影响，网球发射后的轨迹在方程表示的曲线上，其中与发射方向有关．发射器的射程是指网球落地点的横坐标．(Ⅰ)求发射器的最大射程；(Ⅱ)请计算在什么范围内，发射器能将球发过网（即网球飞行到球网正上空时，网球离地距离大于1米）？若发射器将网球发过球网后，在网球着地前，小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球，试问击球点的横坐标最大为多少？并请说明理由．

正确答案

(1)由得：或由，当且仅当时取等号因此，最大射程为20米；

(Ⅱ)网球发过球网，满足时

 所以，即，

因此    

 依题意：关于k的方程 在上有实数解  

即     

得， 此时，球过网了，所以击球点的横坐标 a最大为14

解析

本题是函数的应用，将实际问题与函数联系起来，有利于学生对函数的理解。

考查方向

函数的应用

解题思路

最大射程就是最大值，是网球落地的横坐标

易错点

实际问题和函数模型的转换

知识点

根据实际问题选择函数类型基本不等式的实际应用
1
题型：简答题
|
分值: 10分

22．选修4-1几何证明选讲如图，是圆的直径，点在弧上，点为弧的中点，作于点，与交于点，与交于点．(Ⅰ)证明：；   (Ⅱ)若，求圆的半径．

23. 选修4-4极坐标与参数方程

已知曲线的极坐标方程为,将曲线（为参数）经过伸缩变换后得到曲线．(Ⅰ)求曲线的参数方程；  (Ⅱ)若点在曲线上运动，试求出到曲线的距离的最小值

24选修4-5不等式证明选讲已知函数，且满足（）的解集不是空集．(Ⅰ)求实数的取值集合；   (Ⅱ)若求证：．

正确答案

22.（1）连接，因为点为的中点，故，又因为，是的直径，       

（2）由知 直角中由勾股定理知圆的半径为10 

23. （1）曲线的普通方程是：

（2）曲线的普通方程是：  设点，由点到直线的距离公式得：其中时，，此时

24. （1）要的解集不是空集，则                                  不妨设，则                                 

解析

22. 连接，因为点为的中点，故，         又因为，是的直径，       （2）由知 直角中由勾股定理知圆的半径为10

 23. （1）曲线的普通方程是：（2）曲线的普通方程是：设点，由点到直线的距离公式得：其中时，，此时 

24. 题意说明不等式有解，因此只要大于的最小值即可；（2）要证不等式，由于不等式两边均为正，因此我们采取作商法，两边同除以，只要证，即，而这由幂的知识可得  

考查方向

22.圆周角定理，相似三角形的性质．23. 椭圆的参数方程，坐标变换，点到直线距离公式．24. 不等式有解问题，不等式的证明．

解题思路

22.利用圆周角定理计算，结合相似性质求解 23. 先求出直角坐标系下的椭圆方程，然后得到距离公式，进而判断最值24.利用集合的概念先解出不等式的解集，然后化简求解。

易错点

22.找相似条件  23. 参数方程的坐标转换，最值的判断  24. 基本不等式的应用，不等式的判断

知识点

与圆有关的比例线段

点击 “立即下载”

即可下载本试卷，含解析哦

知道啦