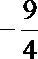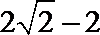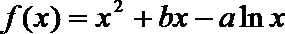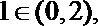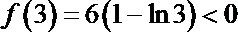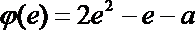- 真题试卷
- 模拟试卷
- 预测试卷
1.设
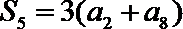
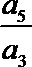
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如果




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在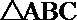
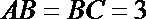
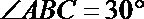
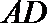
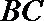
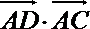
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在△ABC所在平面上有三点P、Q、R,满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知定义在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义域为








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
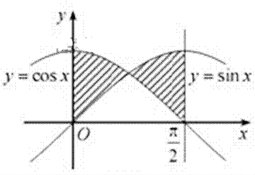
13.由曲线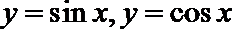
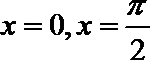
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设



① 
② 
③ 
④ 

⑤ 存在经过点

以上结论正确的是__________________(写出所有正确结论的编号).
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
15.在直角三角形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在△ABC中,角A、B、C所对的边分别为a、b、c, q=(



(1)求sin A的值;
(2)求三角函数式
正确答案
(I)∵

根据正弦定理,得
又



又
(II)原式

∵
∴

∴


解析
解析已在路上飞奔,马上就到!
知识点
18.数列{an}的前n项和为Sn,且Sn=n(n+1)(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:求数列{bn}的通项公式;
(3)令cn=(n∈N*),求数列{cn}的前n项和Tn.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在△ABC中,

(1)求BC的长;
(2)求△DBC的面积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知



(1)求函数

(2)若关于



正确答案
(1)





令



解得
经检验



(2)


设


当



①若



解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(I)若x=2是函数f(x)的极值点,1和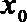
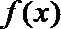
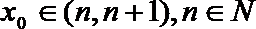
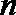
(II)若对任意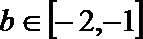
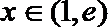
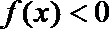
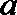
正确答案
(Ⅰ)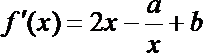
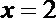

∴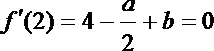
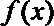
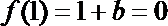
由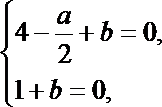
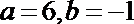
∴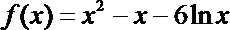
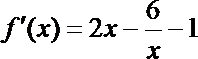
令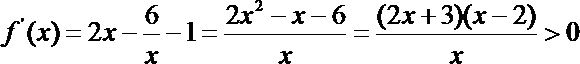
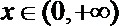
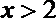
令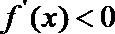
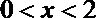
所以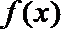
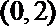
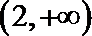
故函数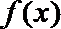
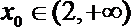
因为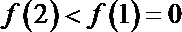
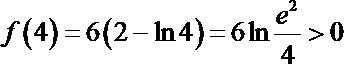
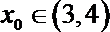
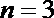
(Ⅱ)令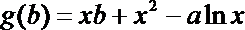
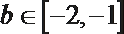
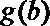
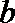
根据题意,对任意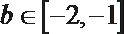
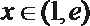
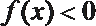
则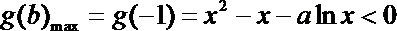
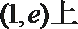
令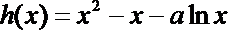
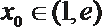
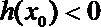
由于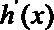
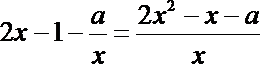
令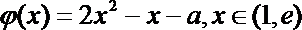
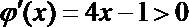
∴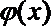
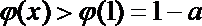
①当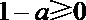
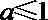
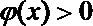
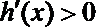
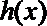
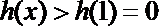
②当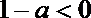
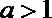
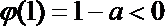
若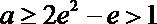
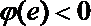
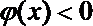
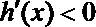
∴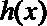
∴存在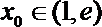
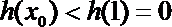
若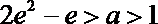
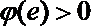
∴在(1,e)上一定存在实数m,使得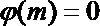
∴在(1,m)上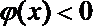
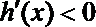
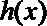
∴存在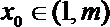
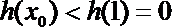
综上所述,当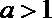
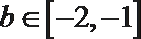
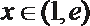
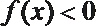
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求函数

(2)求函数
(3)若存在


正确答案
(1)因为函数
所以

又因为



(2)由(1),
因为当


又


故函数

(3)因为存在

而当

所以只要
又因为


所以









因为
令

所以

而



当


所以,当





当





综上可知,所求

解析
解析已在路上飞奔,马上就到!