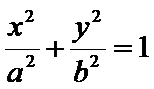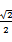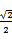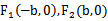- 真题试卷
- 模拟试卷
- 预测试卷
1.已知复数




正确答案
解析
z=





考查方向
解题思路
先从等式中解出 z=


易错点
易在复数与对应点的关系上出错.
知识点
2.已知实数


正确答案
解析
画出可行域,如图,根据目标函数的斜率为

考查方向
解题思路
画出可行域,根据图形解出目标函数的最大值
易错点
可行域画错,目标函数的处理错误。
知识点
3.“


正确答案
解析
命题:“


显然为必要不充分条件,所以选B.
考查方向
解题思路
先解命题:“

易错点
容易将“命题‘

知识点
4.设

正确答案
解析
sin







考查方向
解题思路
将左边化为


易错点
诱导公式,辅助角公式,求解不等式
知识点
5.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周



正确答案
解析
依题意,

考查方向
解题思路
依题意,直接列出等式
易错点
不理解题中“圆堡瑽(圆柱体)的体积为:V=
知识点
7.右图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有 ( )
正确答案
解析
本程序运行执行的是一个分段函数的求值问题,分段函数为:


考查方向
解题思路
本程序执行的是分段函数的求值问题,根据程序框图,写出分段函数,画出函数图像如图所示,可可解出x的值有4个。
易错点
不理解程序框图,不能准确画出图像。
知识点
8.已知等差数列






正确答案
解析
设




考查方向
解题思路
根据等差数列的前n项和,求出通项公式

易错点
由等差数列的前n项和求通项,不理解直线的方向向量
知识点
9.若

正确答案
解析
若f(x)=











考查方向
解题思路
先由偶函数性质,求出a=1,将不等式进行化简整理



易错点
不等式的化简整理
知识点
10.如图所示,函数



正确答案
解析
设两个交点为A、B,由抛物线图象可知,令y=0,解得交点A(-









考查方向
解题思路
先根据两个图像的特殊性,求出两个交点的坐标,AB两点的水平距离恰为1/4周期,应用周期公式求出

易错点
不能正确的提炼图像中渗透的信息,没有掌握抛物线,二次函数图特殊性.
知识点
6.已知双曲线






正确答案
解析
解:由题意可知,




考查方向
解题思路
画出双曲线简图,根据三角形ABF的特点, 点到a,b,c的方程, 再结合双曲线中a,b,c的关系, 求出双曲线的离心率.
易错点
本小题容易在画图和理解,图上出错
知识点
12.已知函数


正确答案
解析
(1).当m=0,n=0时,f(x)=

(2).当m=0,n







考查方向
解题思路
根据函数的特点,从特殊值入手,(1).当m=0,n=0;当m=0,n
易错点
不理解{x| f(x)=0}={x| f(f(x))=0 }
知识点
11.如右下图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的
正确答案
解析
有几何体三视图可知,该纸盒为棱长为















考查方向
解题思路
先讲几何体的三视图,还原成立体图形,得到该纸盒为棱长为
易错点
1. 三视图还原直观图2.不能正确理解“在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动”3. 球与正四面体的切接关系(位置关系与数量关系)
知识点
13.已知


正确答案
2
解析
原式可变为

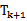









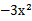


考查方向
解题思路
先展开






易错点
在利用匹配关系中,容易找错

知识点
14.已知抛物线


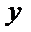



正确答案
2
解析
如图,由题意可得 AF=AC设AF=3m,由AB=2BC,可AB=2m,BC=m,过A作AD垂直x轴于D,设A的横坐标为


考查方向
解题思路
画出抛物线简图,用抛物线定义,结合题中的位置关系,数量关系,求出点A(2,2
易错点
对抛物线定义及性质掌握不熟
知识点
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将
易错点
处理变量之间的整体关系及转化
知识点
16.在






正确答案
2
解析
设AB=a,在三角形ABM中,cosA=











考查方向
解题思路
先将cosA表示为关系是AB边长的关系式,

易错点
根据提供的数据,选择正、余定理,函数的最值讨论
知识点
若等差数列


17.求
18.设数列



正确答案
a=3;
解析
设等差数列


即


解得
考查方向
解题思路
将原式变形


易错点
前n项和与通项的转化
正确答案
见解析
解析
由(1)
考查方向
解题思路
将原式变形


易错点
裂项求和应用不熟练.
如图,矩形










21.求证:

22.求直线

正确答案
证明见解析
解析
连结OM延长交BF于H,则H为BF的中点,又P为BC的中点,∴PH∥CF,又∵CF

解题思路
根据题意,易证PO∥AC,从而证得PH∥平面AFC
易错点
线面平行中,在面中找线,空间向量的计算不准。
正确答案
解析
设直线AC与平面CEF所成角为
A(0,-1,0),C(0,1,1),E(



令a=2,则

所以直线AC与平面CEF所成角的正弦值为
解题思路
以O为原点,AB为y轴,建立空间直角坐标系,利用空间向量直接求角的正弦
易错点
线面平行中,在面中找线,空间向量的计算不准。
随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了了解公众对“延迟退休”的态度,某校课外研究性学习小组对公务员和教师各抽取了50人进行调查,将调查情况进行整理后制成下表:
19.求上表中
20.现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为X,求X的分布列和期望.
正确答案
m=10,n=30, p=30有95%的把握认为“是否同意延迟退休与不同的职业有关.
解析
根据题中提供的数据计算得
所以有95%的把握认为“是否同意延迟退休与不同的职业有关”
考查方向
解题思路
根据列联表的特点,直接求出m=10,n=30,p=30 o;利用公式求出卡方,
易错点
列联表中的原始数据,随机变量的取值及对应的概率
正确答案
所以X的分布列为
EX=1



解析
公务员有4人同意,1人不同意,教师有3人同意,2人不同意.从两个职业人群中各抽取2人,同意延迟退休的人数X的取值为1,2,3,4……………………6分



所以X的分布列为
EX=1



考查方向
解题思路
先统计公务员5个中同意与不同意的人数,再统计教师5中同意与不同意的人数,得到同意延迟退休的人数X的取值为1,2,3,4,然后算对应用的概率.
易错点
列联表中的原始数据,随机变量的取值及对应的概率
已知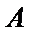
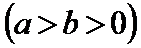
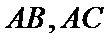
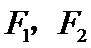
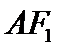
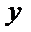
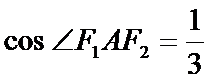
23.求该椭圆的离心率;
24.设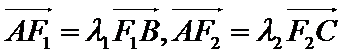
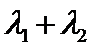
正确答案
.e=
解析
当线段A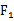
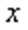
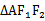
因为cos∠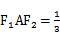

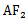


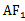
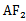
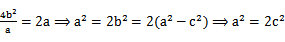
考查方向
解题思路
先证出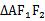
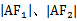
易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
正确答案
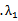
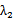
解析
由23得椭圆方程为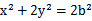
(1) 当AB、AC的斜率都存在时,设,A(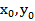
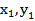
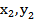
则直线AC的方程为y=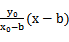
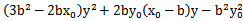
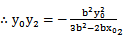
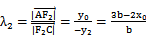
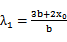
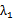
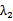
(2) 若AB⊥x轴,则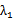
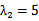
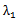
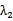
综上所述,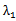
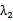
考查方向
解题思路
由23得到含有b的椭圆方程,根据题意对直线AB、AC的斜率进行分为讨论,设出坐标,联立方程组,利用根与系数关系,结合向量关系式,将向量关系转化为坐标关系,用A的坐标及b,表求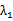
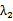
易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
已知函数
25.若


26.若

正确答案
m=0
解析
当




只要满足

对于








对于


则

所以


所以





综上所述可得:
考查方向
解题思路
利用条件,将不等式恒成立问题转化成只要满足

易错点
利用导数在处理单调区间及分类讨论上容易出错;
正确答案
证明见解析
解析
下面用数学归纳法证明
(1)当



(2)假设


只需证明










由归纳假设

若

构造函数





故

由‚及题意知

综合


考查方向
解题思路
用分析法,从结论入手,考虑由于与正整数有关,可以用数学归纳法证明,在证明假设n=k,将












易错点
不容易考虑到用数学归纳法证明
选修4-1: 几何证明选讲.
如图所示,已知










27.求证:
28.若

正确答案
见解析
解析
∵














考查方向
解题思路
先证明

易错点
找不准三角形相似或全等的条件
正确答案
PA=
解析
∵



由27题可知:







考查方向
解题思路
先综合题中条件及27中结论,解出EP=

易错点
找不准三角形相似或全等的条件