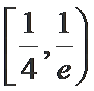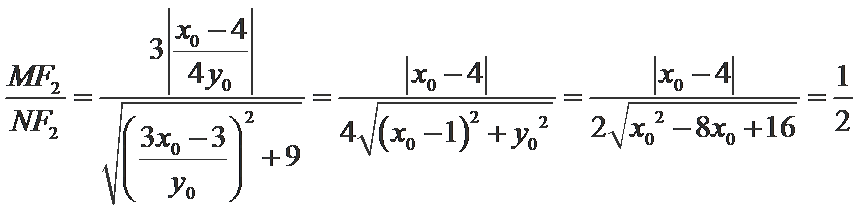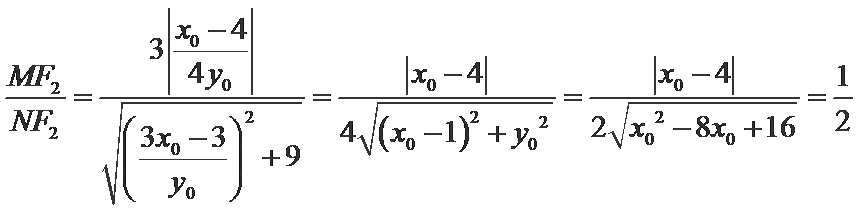- 真题试卷
- 模拟试卷
- 预测试卷
6.已知等差数列



正确答案
2
解析
设







考查方向
解题思路
本题考查运用等差数列及等比数列性质求首项,解题步骤如下:设







易错点
本题必须注意审题,忽视则会出现错误。
知识点
10.已知双曲线


正确答案
解析
将


考查方向
解题思路
本题考查运用双曲线的渐近线方程及抛物线的准线方程,求a,b,解题步骤如下:将



易错点
本题必须注意审题,忽视则会出现错误。
知识点
7.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球中有黄球的概率为___________
正确答案
解析
考查方向
解题思路
本题考查运用乘法原理求这2只球中没有黄球的概率,再利用互斥事件的性质求解。解题步骤如下:
易错点
本题必须注意审题,忽视则会出现错误。
知识点
8.圆锥的侧面展开图是圆心角为π,面积为2π的扇形,则圆锥的体积是___________
正确答案
解析
2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
考查方向
解题思路
本题考查运用圆锥侧面积求底面半径及母线,再求高,进而求体积。解题步骤如下:2πr=πl, 2π=πrl.得:r=,l=2,h=1.V=π
易错点
本题必须注意审题,忽视则会出现错误。
知识点
9.已知

正确答案
解析
-(cos2x-sin2x)=-2cos(2x+




考查方向
解题思路
本题考查运用辅助角公式求辅助角,解题步骤如下:
先用辅助角公式得-2cos(2x+



易错点
本题必须注意
知识点
5.阅读下面的程序框图,运行相应的程序,则输出i的值为___________;
正确答案
4
解析
i=1,a=2,i=2,a=5,i=3,a=16,i=4,a=65,输出i=4
考查方向
解题思路
本题考查运用程序框图循环语句求解
易错点
本题必须注意所求的是i,忽视则会出现错误。
知识点
1.函数y=
正确答案
(-1,+∞)
解析
x+1>0,x>-1, (-1,+∞)
考查方向
解题思路
本题考查采用正确的方法求定义域的方法和不等式求解的能力,解题步骤如下:
分式有意义与二次根式有意义要求x+1>0,从而求出结果
易错点
本题必须注意分式有意义和二次根式有意义双重约束条件和定义域的区间表示,忽视则会出现错误。
知识点
3.“


正确答案
充分不必要
解析
a(a-1)-6=0,a=3或a=-2,经检验,均符合。a=3→a=3或a=-2,充分不必要条件。
考查方向
解题思路
本题先考查采用正确的方法求直线平行的条件,又考查命题的充要条件,解题步骤如下:
a(a-1)-6=0,a=3或a=-2,经检验,均符合。a=3→a=3或a=-2,充分不必要条件。
易错点
本题必须注意哪个是题设,哪个是结论,忽视则会出现错误。
知识点
2.设




正确答案
1
解析
z=(1-i)/(1+i)=-i,
考查方向
解题思路
本题先考查采用正确的方法求复数,又考查复数的模的求法,解题步骤如下:
z=(1-i)/(1+i)=-i,
易错点
本题必须注意求的是复数的模,而不是复数本身,忽视则会出现错误。
知识点
4.若样本数据








正确答案
16
解析
2*8=16
考查方向
解题思路
本题考查采用标准差与数据关系的结论:只与系数相关。解题步骤如下:2*8=16
易错点
本题必须注意标准差含义,忽视则会出现错误。
知识点
11.已知菱形






正确答案
2
解析


考查方向
解题思路
本题考查运用平面向量在几何中的应用,解题步骤如下:建立如图所示直角坐标系,
则

易错点
本题必须注意审题,忽视则会出现错误。
知识点
12.如果函数

正确答案
18
解析



















考查方向
解题思路
本题考查运用函数的单调性解决不等式问题,解题步骤如下:分三种情况讨论。
详解见解析。
易错点
本题必须注意分类讨论,忽视则会出现错误。
知识点
14.已知圆O:
正确答案
解析
设AC中点P(x,y)OP⊥AP,
AC=2PM,PM∈[

考查方向
解题思路
本题考查运用曲线的方程与几何图形知识解决问题的能力,先设AC中点P(x,y)OP⊥AP,AP=
AC=2PM,PM∈[

易错点
本题必须运用几何性质找曲线的方程,否则无从下手。
知识点
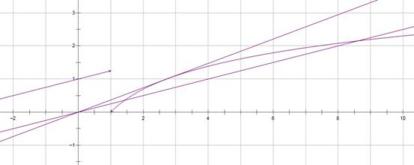
13.已知函数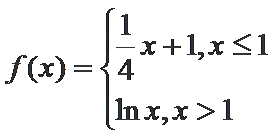
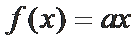
取值范围是___________
正确答案
解析
∵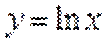
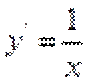
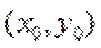
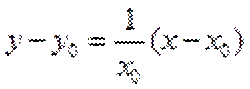
∴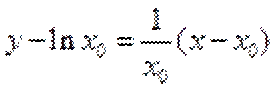
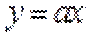
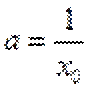
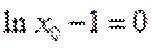
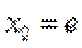
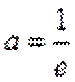
当直线与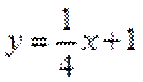
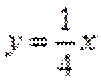
当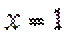
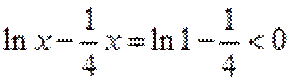
当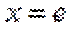
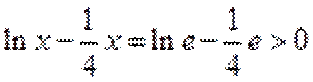
当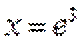
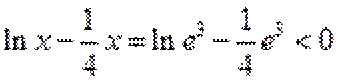
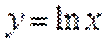
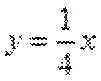
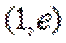
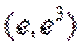
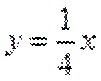
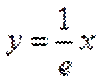
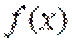
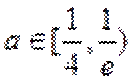
考查方向
解题思路
本题考查运用导数解决函数的能力,解题步骤如下: 先求导,找函数的切线方程,再利用零点的判定方法,找到a的取值范围。
易错点
本题必须注意审题,忽视则会出现错误。
知识点
16.在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2
(1)求证:AC⊥PB;
(2)若PC=2,点M是棱PB上的点,且CM∥平面PAD,求BM的长。
正确答案
见解析
解析
(1)∵PC⊥平面ABCD,∴PC⊥AC,
又∠CBA=30°,BC=2
∴AC=
=
∴AC2+BC2=4+12=16=AB2,∴∠ACB=90°,
故AC⊥BC.又∵PC、BC是平面PBC内的两条相交直线,
故AC⊥平面PBC,∴AC⊥PB.
(2) BM=2
考查方向
解题思路
(1)由余弦定理求AC
(2)由勾股逆定理得∠ACB=90°
(3)AC⊥BC,PC⊥AC,AC⊥平面PBC,∴AC⊥PB
易错点
证明过程不到位。
知识点
17. 某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油 




(1)试写出第


(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定
正确答案
见解析
解析
解:(1)
(2)根据题意
所以
即 
考查方向
解题思路
本题考查函数不等式的应用.解题步骤如下:
(1)求出函数表达式。
(2)根据函数值域,列出不等式。
(3)用换元法求出
易错点
不等式恒成立分析不够
知识点
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
23.为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加。现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名。从这8名运动员中随机选择4人参加比赛.
(1)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件A发生的概率;
(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
正确答案
见解析
解析
(1)由已知,有
所以事件

(2)随机变量
所以随机变量
所以随机变量
考查方向
解题思路
1利用已知条件把“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会的组合数求出,进而求出概率
易错点
本题必须注意审题,否则求解错误。
知识点
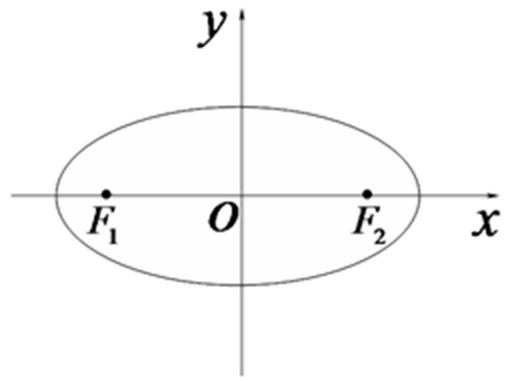
18. 平面直角坐标系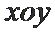
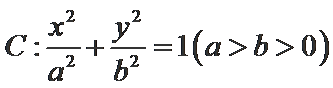
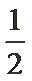
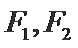
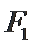
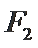
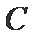
(1)求椭圆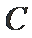
(2)过椭圆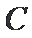
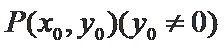
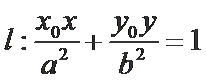
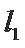
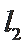
①设直线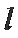
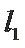
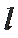

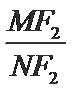
②若连接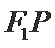
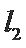
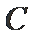
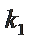
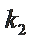
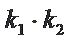
正确答案
见解析
解析
(1)由题意知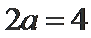
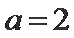
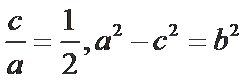
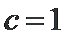
所以椭圆C的标准方程为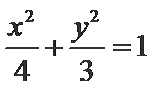
(2)①M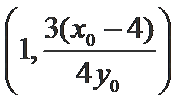
②点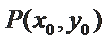
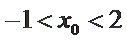
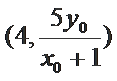
∵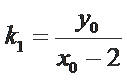
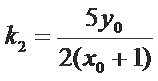
∴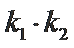
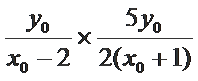

∵点P在椭圆C上, ∴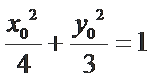
∴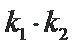
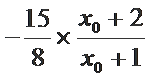
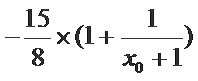
∵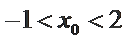
∴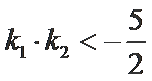
∴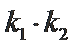
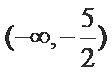
考查方向
解题思路
本题考查导数的性质,解题步骤如下:
(1)根据离心率和几何特点,求出椭圆方程
(2)表示M,N进而得
(3)表示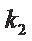
易错点
点M,N表示不当
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
22.(2) [选修4-4:坐标系与参数方程]
在直角坐标系








(1)求

(2)若






正确答案
见解析
解析
(1)
(2)曲线






所以
当


考查方向
解题思路
(1)利用已知条件把

(2)把
易错点
本题必须注意把

知识点
24.若抛物线C的顶点在坐标原点O,其图象关于x轴对称,且经过点M(2,2).
(1)求抛物线C的方程;
(2)过点M作抛物线C的两条弦MA,MB,设MA,MB所在直线的斜率分别为
当

正确答案
见解析
解析
(1)
(2)
定点(6,-4)
考查方向
解题思路
1利用已知条件把求出抛物线方程2.设出直线方程证明其过定点。
易错点
本题必须注意审题,否则求解错误。
知识点
21.(1) [选修4-2:矩阵与变换]
已知



(1)求矩阵
(2)若矩阵
正确答案
见解析
解析
解:(1)
(2)
考查方向
解题思路
1利用已知条件求矩阵A,2由矩阵A,求矩阵A-1,3由矩阵A-1,矩阵
易错点
本题必须注意审题,否则求解错误。