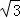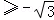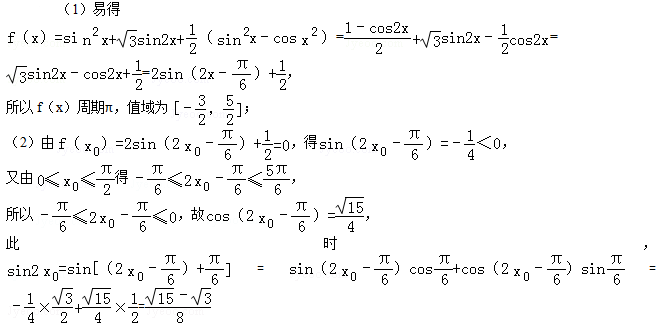- 真题试卷
- 模拟试卷
- 预测试卷
4.过点(1,0)且倾斜角是直线2x+3y+3=0的倾斜角的两倍的直线方程是( )
正确答案
12x+5y-12=0
解析
直线2x+3y+3=0的斜率为k=

过点(1,0)的倾斜角为2α,其斜率为tan2α=


故所求直线方程为:y=
故答案为:12x+5y-12=0
知识点
2.设集合
正确答案
{x|-1<x<1}
解析



故答案为:{x|-1<x<1}
知识点
7.设a∈R,则“a=1”是“直线l1:ax+2y-1=0与l2:x+(a+1)y+4=0平行”的( )条件。(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
正确答案
充分不必要
解析
因为“a=1”时,“直线l1:ax+2y-1=0与l2:x+(a+1)y+4=0”
化为l1:x+2y-1=0与l2:x+2y+4=0,显然两条直线平行;
如果“直线l1:ax+2y-1=0与l2:x+(a+1)y+4=0平行”
必有a(a+1)=2,解得a=1或a=-2,
所以“a=1”是“直线l1:ax+2y-1=0与l2:x+(a+1)y+4=0平行”的充分不必要条件.
故答案为:充分不必要。
知识点
6.设ω>0,函数

正确答案
解析
∵函数

∴

∴ω=n×
又ω>0,故其最小值是
故答案为
知识点
9.若
正确答案


解析
∵

∴

解之得

故答案为:

知识点
8.设点P是曲线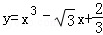
正确答案
[0°,90°]∪[120°,180°)
解析
设点P是曲线
∵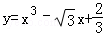
∴点P处的切线的斜率k=3x2﹣
∴k
∴切线的倾斜角α的范围为:[0°,90°]∪[120°,180°)
故答案为:[0°,90°]∪[120°,180°)
知识点
1.已知复数
正确答案
-1
解析
复数
它是纯虚数,所以m=-1
故答案为:-1
知识点
5.下边是根据所输入的x值计算y值的一个算法程序,若x依次取数列
正确答案
1
解析
分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算分段函数
即y=1+|x|的函数值
知识点
3.函数
正确答案
[0,
解析
∵0≤x≤
∴


由


0≤x≤
故f(x)的单调递增区间为[0,
知识点
13.已知关于x的实系数一元二次不等式ax2+bx+c≥0(a<b)的解集为R,则
正确答案
8
解析
由题意,ax2+bx+c≥0(a<b)的解集为R,
则必有△=b2﹣4ac≤0,a>0,
对于


令
则
故答案为8
知识点
10.如图,l1,l2,l3是同一平面内的三条平行直线,l1与l2间的距离是1,l3与l2间的距离是2,正△ABC的三顶点分别在l1,l2,l3上,则△ABC的边长是( )
正确答案
解析
如图,过A,C作AE,CF垂直于L2,点E,F是垂足,
将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处,延长DA交L2于点G.
由作图可知:∠DBG=60°,AD=CF=2.
在Rt△BDG中,∠BGD=30°.在Rt△AEG中,∠EAG=60°,AE=1,AG=2,DG=4.
∴BD=
在Rt△ABD中,AB=
故答案为:
知识点
11.已知△ABC中,AB边上的中线CM=2,若动点P满足

正确答案
-2
解析
由题意可得:
∴
所以P、M、C三点共线,即点P在CM上,
而


=2

∵



故答案为:-2
知识点
12.已知等差数列{an}的前n项和为Sn,若(a2-1)3+2010(a2-1)=1,(a2009-1)3+2010(a2009-1)=-1,则下列四个命题中真命题的序号为( )
①S2009=2009;
②S2010=2010;
③a2009<a2;
④S2009<S2.
正确答案
②③
解析
由(a2-1)3+2010(a2-1)=1,(a2009-1)3+2010(a2009-1)=-1
可得a2-1>0,-1<a2009-1<0即a2>1,0<a2009<1,从而可得等差数列的公差d<0
③a2009<a2正确
把已知的两式相加可得(a2-1)3+2010(a2-1)+(a2009-1)3+2010(a2009-1)=0
整理可得(a2+a2009-2)•[(a2-1)2+(a2009-1)2-(a2-1)(a2009-1)+2010]=0
结合上面的判断可知(a2-1)2+(a2009-1)2-(a2-1)(a2009-1)+2010>0
所以a2+a2009=2,而
由于d<0,a2010<a2009<1,则S2009=S2010-a2010=2010-a2010>2009①错误
由公差d<0 可得a2+a2008>a2+a2009>a2+a2010,结合等差数列的列的性质,可得2a1005>2>2a1006
从而可得0<a1006<1<a1005
④s2009-s2=a3+a4+…+a2009=2007a1006>0,故④错误
故答案为:②③
知识点
14.已知二次函数f(x)=x2-x+k,k∈Z,若函数g(x)=f(x)-2在

正确答案
解析
若函数g(x)=x2-x+k-2在
∴二次函数f(x)=x2-x+2,其值域f(x)∈[




当且仅当f(x)=

而

∴当f(x)=


故答案为:
知识点
19.某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质。已知每投放质量为m的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足
(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定该投放的药剂质量m的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数f(x)=x+

(1)求a的值。
(2)问:|PM|•|PN|是否为定值?若是,则求出该定值;若不是,请说明理由。
(3)设O为坐标原点,求四边形OMPN面积的最小值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求f(x)的最小正周期和值域;
(2)若x=x0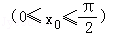
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设△ABC的三个内角A,B,C所对的边分别为a,b,c,且满足
(Ⅰ)求角B的大小;
(Ⅱ)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数f(x)=ax3+bx2+(b-a)x(a,b不同时为零的常数),导函数为f′(x)。
(1)当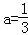
(2)求证:函数y=f′(x)在(-1,0)内至少有一个零点;
(3)若函数f(x)为奇函数,且在x=1处的切线垂直于直线x+2y-3=0,关于x的方程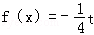
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数


(1)求证:P点的纵坐标为定值,并求出这个值;
(2)若
(3)记Tn为数列

正确答案
解析
解析已在路上飞奔,马上就到!