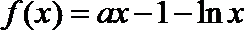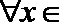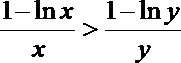- 真题试卷
- 模拟试卷
- 预测试卷
1.如图所示的韦恩图中,







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如右图,在△





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数
①当c=0时,有
②当b=0,c>0时,方程
③函数
④当x>0时;函数


其中正确的命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知正方形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知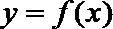
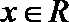
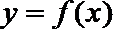
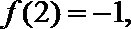
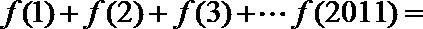
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如右图过抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.定义在R上的可导函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图所示是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2,侧视图是一直角三角形,俯视图为一直角梯形,且AB=BC=1,则异面直线PB与CD所成角的正切值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知定义在



正确答案
(
解析
解析已在路上飞奔,马上就到!
知识点
16.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
17.在△ABC中,内角A、B、C所对边的长分别为a、b、c,已知向量



(1)求A的大小;
(2)若a=
正确答案
(1)

(2)a=
得a2=(b+c)2-2bc-2bccosA
∵b+c=3,
∴3=9-3bc,bc=2
由
得
解析
解析已在路上飞奔,马上就到!
知识点
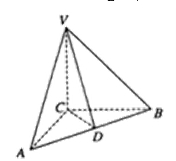
18.如图所示,在三棱锥V—ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=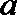
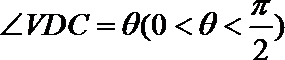
(1)求证:平面VAB⊥平面VCD;
(2)当角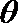
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为



(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数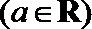
(1)若函数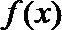
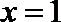
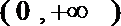
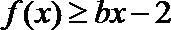
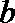
(2)当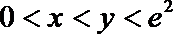
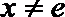
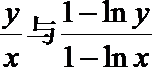
正确答案
(1)∵函数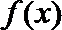
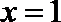
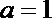
∴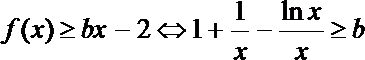
令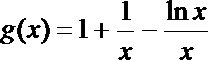
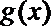
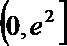
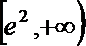
∴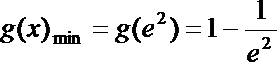
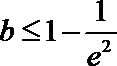
(2)由(Ⅱ)知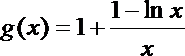
∴0<x<y<e2时,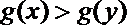
当0<x<e时,1-lnx>0,∴y(1-lnx)>x(1-lny), ∴
当e<x<e2时,1-lnx<0,∴y(1-lnx)>x(1-lny), ∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线






(Ⅰ)判断点F是否在直线BD上;
(Ⅱ)设

正确答案
设




(Ⅰ)将


直线

即
令


(Ⅱ)由①知
因为 


所以
又由①知
故直线BD的斜率
因而直线BD的方程为
因为KF为




由


故圆M的半径
所以圆M的方程为
解析
解析已在路上飞奔,马上就到!
知识点
20.已知直线

(Ⅰ)若椭圆的离心率为
(Ⅱ)若向量


正确答案
(Ⅰ)
∴椭圆的方程为
联立
(II)

整理得
整理得:

由此得
故长轴长的最大值为
解析
解析已在路上飞奔,马上就到!