- 真题试卷
- 模拟试卷
- 预测试卷
3.一扇形的中心角为2,中心角所对的弦长为2,则此扇形的面积为__________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数f (x)=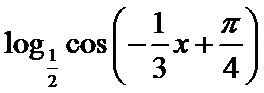
正确答案
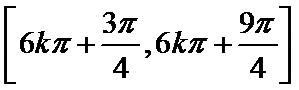
解析
解析已在路上飞奔,马上就到!
知识点
10.已知






正确答案
解析
B=600,A+C=1200, C=1200 -A,
∴ sinA-sinC+
=



∴sin(A-60°)[1-
∴sin(A-60°)=0或sin(A-60°)=
又0°<A<120°
∴A=60°或105°
当A=60°时,S△=


当A=105°时,S△=
知识点
8. 下列命题正确的是____________(只须填写命题的序号即可)
(1)函数
(2)在


(3)当


(4)要得到函数


正确答案
(1)(3)
解析
解析已在路上飞奔,马上就到!
知识点
9.函数


正确答案
解析
已知条件实际上给出了一个在区间
任取

则不等式
即
化简得
由
可知:
所以
上式恒成立的条件为:

由于
且当

所以 
从而 
有 
故

知识点
7.若

正确答案
-8
解析
令

知识点
6.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.电流强度



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.由下列条件解
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设全集
(1)解关于


(2)记




正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量,




正确答案
解法一:
由已知
得
又
所以
解法二:

由已知
得
解析
解析已在路上飞奔,马上就到!
知识点
20.设





(1)求

(2)求函数
(3)当




正确答案
(1)
(2)

(3)
所以
因此


故
猜测
解析
解析已在路上飞奔,马上就到!
知识点
19.已知


(1)推算
(2)求证:
正确答案
如图所示,设
则
同理:

即



又
故

又

整理得 
(1)因

可知

故
(2)


即
解析
解析已在路上飞奔,马上就到!
知识点
18.一个直角走廊宽为

正确答案
设AB所在直线与走廊外轮廓线交于点
又设


而
令
则
又

令







从而CD的最小值是
故平板车的长度不能超过(
解析
解析已在路上飞奔,马上就到!