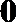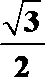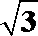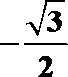理科数学 2012年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

4．下列4个命题:

（1）命题“若，则”；

（2）“”是“对任意的实数，成立”的充要条件；

（3）设随机变量服从正态分布N（0，1），若；

（4）命题“，”的否定是：“，”；

其中正确的命题个数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

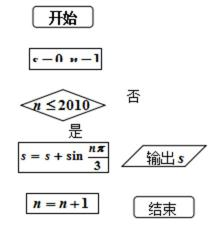
6．阅读如图所示的程序框图，输出的结果的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：单选题

分值: 5分

7．已知集合N，，在集合中随机取两个点．，则P、Q两点在同一反比例函数图象上的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

1．若集合则满足条件的实数x的个数有（）

A1个

B2个

C3个

D4个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

2．函数的定义域是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3.下图是各条棱长均为2的正四面体的三视图，则正（主）视图三角形的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．设函数在处取得极值，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8．若， > 0，且，则的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

9．已知定义在上的函数是奇函数且满足，，数列满足，且，（其中为的前项和）。则（）

A-3

B-2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

10．下图为函数轴和直线分别交于点P、Q，点N（0，1），若△PQN的面积为b时的点M恰好有两个，则b的取值范围为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共8小题，每小题5分，共40分。把答案填写在题中横线上。

题型：填空题

分值: 5分

14.如图所示，已知F1，F2是椭圆的左．右焦点，点P在椭圆C上，线段PF2与圆相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为_______________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 12分

16．已知

（1）求的最大值，及当取最大值时x的取值集合。

（2）在三角形ABC中，a，b，c分别是角A，B，C所对的边，对定义域内任意x，有，若，求的最大值。

正确答案

解：（1）

（2）因为对定义域内任一x有

∴=

最大为

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 12分

17．某学校要用三辆校车从老校区把教职工接到校本部，已知从老校区到校本部有两条公路，校车走公路①堵车的概率为，不堵车的概率为；校车走公路②堵车的概率为，不堵车的概率为．若甲．乙两辆校车走公路①，丙校车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响．

（1）若三辆校车中恰有一辆校车被堵的概率为，求走公路②堵车的概率；

（2）在（1）的条件下，求三辆校车中被堵车辆的辆数的分布列和数学期望．

正确答案

解：（1）由已知条件得

即，则

答：的值为．

（2）解：可能的取值为0，1，2，3

的分布列为：

所以

答：数学期望为．

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：填空题

分值: 12分

18.如图，在三棱柱中，所有的棱长都为2，．

（1）求证：；

（2）当三棱柱的体积最大时，求平面与平面所成的锐角的余弦值。

正确答案

解:（1）证明：取的中点，连接，

在三棱柱中，所有棱长都为2，

则，所以平面

而平面，故

（2）当三棱柱的体积最大时，点到平面的距离最大，此时平面．

设平面与平面的交线为，

在三棱柱中，，平面，则，

过点作交于点，连接．由，知平面，

则，故为平面与平面所成二面角的平面角。

在中，,则

在中，，,

即平面与平面所成锐角的余弦值为。

另解：当三棱柱的体积最大时，点到平面的距离最大

此时平面．以所在的直线分别为轴，建立直角坐标系

依题意得．

由得，设平面的一个法向量为

而，则，取

而平面，则平面的一个法向量为

于是，

故平面与平面所成锐角的余弦值为。

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

11．已知，且，那么的展开式中的常数项为_______________。

正确答案

-540

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

12．如图，在直角梯形中，，，，，点是梯形内（包括边界）的一个动点，点是边的中点，则的最大值是_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 5分

13．设实数满足不等式组，则的最小值为_______________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

15．数列{}的前n项和为，若数列{}的各项按如下规律排列：，，，，，，，，，…，，，…，，…有如下运算和结论：

①;

②数列a1，a2＋a3，a4＋a5＋a6，a7＋a8＋a9＋a10，…是等比数列；

③数列a1，a2＋a3，a4＋a5＋a6，a7＋a8＋a9＋a10，…的前n项和为＝；

④若存在正整数，使，则．

其中正确的结论是___________（将你认为正确的结论序号都填上）

正确答案

①③④

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

简答题（综合题）本大题共39分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．已知函数

（1）若在区间单调递增，求a的取值范围；

（2）若—1＜a＜3，证明：对任意都有＞1成立．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

20．如图，已知抛物线的准线为,焦点为．⊙M的圆心在轴的正半轴上,且与轴相切．过原点作倾斜角为的直线,交于点, 交⊙M于另一点,且．

（1）求⊙M和抛物线的方程；

（2）若为抛物线上的动点,求的最小值；

（3）过上的动点向⊙M作切线,切点为,求证：直线恒过一个定点,并求该定点的坐标．

正确答案

解：（1）因为,即,所以抛物线C的方程为．

设⊙M的半径为,则,所以的方程为

（2）设,则=

所以当时, 有最小值为2

（3）以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦

设点,则,所以⊙Q的方程为

从而直线QS的方程为(*)

因为一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

分值: 14分

21．设为数列的前项和，对任意的，都有（为常数，且）．

（1）求证：数列是等比数列；

（2）设数列的公比，数列满足，N，求数列的通项公式；

（3）在满足（2）的条件下，求证：数列的前项和。

正确答案

解：（1）证明：当时，，解得

当时，．即

∵为常数，且，∴

∴数列是首项为1，公比为的等比数列…

（2）解：由（1）得，，

∵

∴，即

∴是首项为，公差为1的等差数列

∴，即（N）

（3）证明：由（2）知，则．

∴，

当时，，

∴

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷