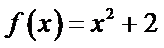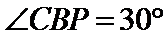- 真题试卷
- 模拟试卷
- 预测试卷
1.设函数


正确答案
解析
由





考查方向
解题思路
集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.
易错点
交集的定义与应用
2.已知

正确答案
解析
由


考查方向
解题思路
复数


易错点
复数的乘除运算
4.已知x,y满足

正确答案
解析
由


当其经过直线




考查方向
解题思路
作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到结论.
易错点
z的几何意义
5.为了研究某班学生的脚长







正确答案
解析

考查方向
解题思路
直接根据回归方程的公式,由所给的数据代入就求出回归方程,再将
易错点
求线性回归方程时在严格按照公式求解时,一定要注意计算的准确性.
9.在








正确答案
解析
所以
考查方向
解题思路
首先用两角和的正弦公式转化为含有



易错点
解三角形中边角之间的互化
3.已知命题p:

正确答案
解析
试题分析:由



考查方向
解题思路
首先明确各命题的真假,利用或、且、非真值表,进一步作出判断.
易错点
简易逻辑联结词的运用
6.执行两次右图所示的程序框图,若第一次输入的




正确答案
解析
第一次

考查方向
解题思路
通过程序框图的要求,写出每次循环的结果得到输出的值.
易错点
循环结构的条件判断
7.若

正确答案
解析

考查方向
解题思路



易错点
比较大小的中间量
8.从分别标有




正确答案
解析

考查方向
解题思路
直接由排列数得出
易错点
排列数的灵活运用
10.已知当



正确答案
解析
当







.
考查方向
解题思路
当

易错点
函数的图象、函数与方程及函数性质的综合应用.
11.已知



正确答案
解析
由二项式定理的通项公式



考查方向
解题思路
根据二项式展开式的通项,确定二项展开式中的指定项,
易错点
由二项式定理求通项
13.由一个长方体和两个
正确答案
解析
该几何体的体积为
考查方向
解题思路
根据三视图想象出空间几何体的形状并画出其直观图.根据几何体的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据,利用面积或体积公式计算即可.
易错点
根据三视图判断几何体的形状及数据所对应的几何量
14.在平面直角坐标系





正确答案
解析
考查方向
解题思路
先由抛物线的定义及焦点弦得出


易错点
两个二次曲线联立得出一元二次方程
15.若函数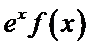
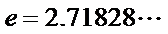
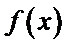
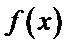
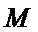
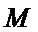
①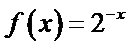
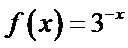
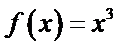
正确答案
①④
解析
①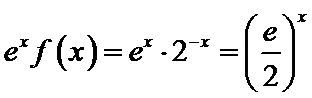
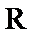
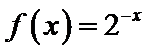
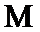
②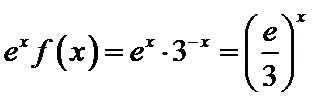
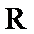
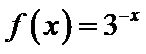
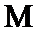
③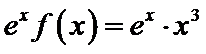
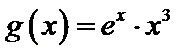
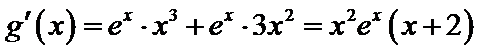
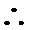
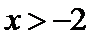
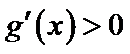
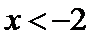
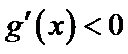
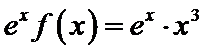
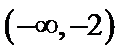
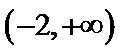
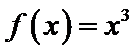
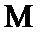
④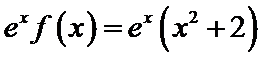
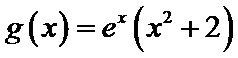
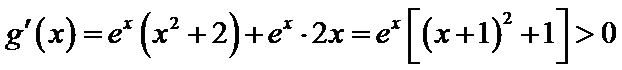
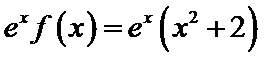
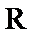
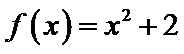
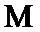
考查方向
解题思路
创新题,利用题中所给新定义的概念依次对①、②、③、④个选项分析转化成熟悉的知识进而得出结果.
易错点
创新题中新定义的理解与转化
12.已知




正确答案
解析





考查方向
解题思路
利用平面向量的数量积求出两向量的数量积,再计算两个向量的模,进而应用平面向量的夹角公式,建立
易错点
利用向量的模与向量数量积运算的灵活转换
20.(本小题满分13分)
已知函数


(Ⅰ)求曲线

(Ⅱ)令

正确答案
(Ⅰ)
解析
(Ⅰ)由题意
又
所以
因此 曲线


即 
(Ⅱ)由题意得 
因为

令
则
所以

因为
所以 当
当
(1)当
当


当


所以 当


(2)当
由 

①当

当


当


当


所以 当

极大值为
当


②当

所以 当



③当
所以 当


当


当


所以 当


当

极小值是
综上所述:
当



函数

当






极大值是
极小值是
当


当



在

极大值是
极小值是
考查方向
解题思路
(Ⅰ)求导数得斜率









易错点
应用导数研究函数的单调性、极值,导数的综合应用
18.(本小题满分12分)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
正确答案
(I)
解析
(I)记接受甲种心理暗示的志愿者中包含

(II)由题意知X可取的值为:
因此X的分布列为
X的数学期望是
=
考查方向
解题思路
(I)记接受甲心理暗示的志愿者中包含

易错点
随机变量的分布列的灵活运用
19.(本小题满分12分)
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)如图,在平面直角坐标系xOy中,依次连接点P1(x1, 1),P2(x2, 2)…Pn+1(xn+1, n+1)得到折线P1 P2…Pn+1,求由该折线与直线y=0,

正确答案
(I)
解析
(I )设数列
由题意得

因为q>0,所以
因此数列
(II)过




由(I)得
记梯形

由题意
所以
=

又



所以
考查方向
解题思路
(I)依题意列出




易错点
列方程组解首项与公比及错位相减法求和.
16.设函数


(Ⅰ)求
(Ⅱ)将函数




正确答案
(Ⅰ)

解析
(Ⅰ)因为
所以
由题设

故
所以
(Ⅱ)由(Ⅰ)得
所以
因为
所以
当
即


考查方向
解题思路
(I)利用两解和与差的三角函数化简得到




根据

易错点
三角函数图象的变换与性质的灵活运用
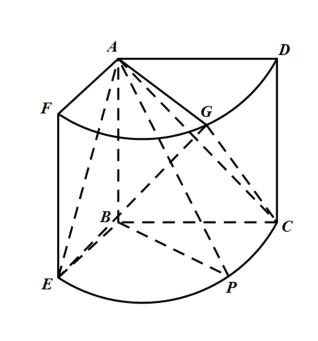
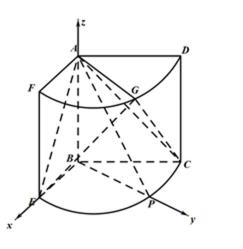
17.如图,几何体是圆柱的一部分,它是由矩形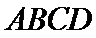
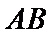
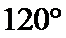
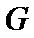
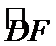
(Ⅰ)设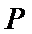
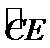
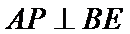
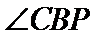
(Ⅱ)当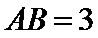
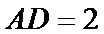
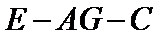
正确答案
(Ⅰ)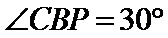
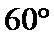
解析
(Ⅰ)因为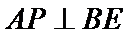
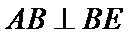
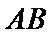
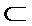
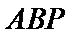
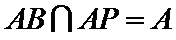
所以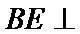
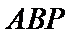
又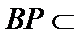
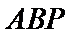
所以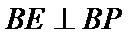
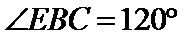
因此
(II)以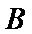
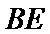
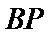
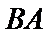
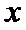
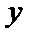
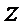
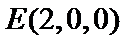
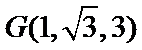
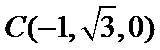
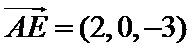
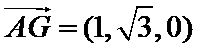
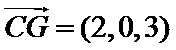
设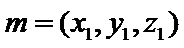
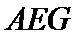
由
取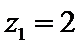
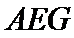
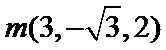
设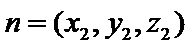
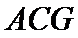
由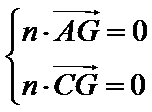
取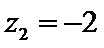
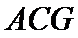
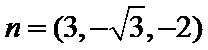
所以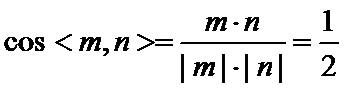
因此所求的角为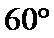
考查方向
解题思路
(I)利用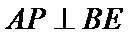
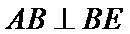
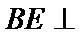
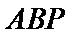
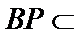
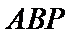
所以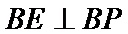
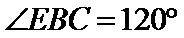
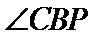
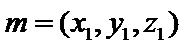
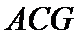
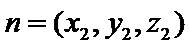
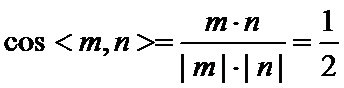
21.(本小题满分14分)
在平面直角坐标系




(Ⅰ)求椭圆
(Ⅱ)如图,动直线


















正确答案
(I)




解析
(I)由题意知 

所以 
因此 椭圆

(Ⅱ)设
联立方程
得
由题意知
且
所以 
由题意可知圆

由题设知
所以
由此直线

联立方程
得
因此 
由题意可知 
而

令
则
因此 
当且仅当


所以 
因此
所以 

综上所述:



考查方向
解题思路
(I)由





易错点
直线与圆锥曲线的联立