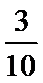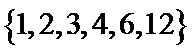- 真题试卷
- 模拟试卷
- 预测试卷
4.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数




正确答案
(1,3)
解析
解析已在路上飞奔,马上就到!
知识点
10.解方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.无穷数列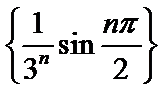
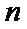
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合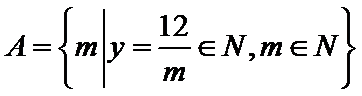
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,在






正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
11.直线


正确答案
(-2,3)
解析
解析已在路上飞奔,马上就到!
知识点
13.已知三个实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.当


正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
16.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.对于定义在R上的函数
①若

②若函数


③若对

④函数

其中正确结论有( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数


正确答案


若

此时,

又





解析
解析已在路上飞奔,马上就到!
知识点
20.甲.乙两地相距



(1)将全程运输成本

(2)为了使全程运输成本最小,货车应以多大的速度行驶.
正确答案
(1)
(2)







当
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列






(1)求
(2)若数列




正确答案
(1)

所以
(2)
因为

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(1)设


(2)设计一个函数


(3)








正确答案
(1)
∴
(2)
若
则
(3)
因为且
且
因为
所以

由正弦定理得



所以
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数
(1)作出函数



(2)关于


(3)关于



正确答案
(1)解:
(作图如下:)
已知当

(2)

即方程
当
(3)关于



数形结合可知必有

令



解析
解析已在路上飞奔,马上就到!