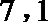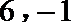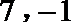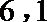- 真题试卷
- 模拟试卷
- 预测试卷
7.某学生四次模拟考试时,其英语作文的减分情况如下表:
显然所减分数y与模拟考试次数x之间有较好的线性相关关系,则其线性回归方程为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 任取



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数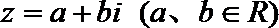
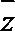
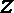
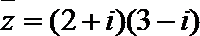
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若方程


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知直线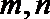
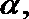
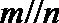
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.二项式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知P是双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.下图是“二分法”解方程的流程图.在①~④处应填写的内容分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.为了测量一古塔的高度,某人在塔的正西方向的A地测得塔尖的仰角为45°,沿着A向北偏东30°前进100米到达B地(假设A和B在海拔相同的地面上),在B地测得塔尖的仰角为
正确答案
50
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在平面直角坐标系中,




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.用一个边长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(Ⅰ)求

(Ⅱ)是否存在实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在底面为直角梯形的四棱锥






(1)求证:
(2)求直线

(3)设点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.符合下列三个条件之一,某名牌大学就可录取:
①获国家高中数学联赛一等奖(保送录取,联赛一等奖从省高中数学竞赛优胜者中考试选拔);
②自主招生考试通过并且高考分数达到一本分数线(只有省高中数学竞赛优胜者才具备自主招生考试资格);
③高考分数达到该大学录取分数线(该大学录取分数线高于一本分数线).
某高中一名高二数学尖子生准备报考该大学,他计划:若获国家高中数学联赛一等奖,则保送录取;若未被保送录取,则再按条件②、条件③的顺序依次参加考试.
已知这名同学获省高中数学竞赛优胜奖的概率是0.9,通过联赛一等奖选拔考试的概率是0.5,通过自主招生考试的概率是0.8,高考分数达到一本分数线的概率是0.6,高考分数达到该大学录取分数线的概率是0.3.
(I)求这名同学参加考试次数

(II)求这名同学被该大学录取的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆E: 


(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在22~24题中任选一题作答
22.选修4-1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE=EF.
23.选修4-4:坐标系与参数方程
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为
(I)求圆C的极坐标方程;
(II)



24.选修4-5:不等式选讲
已知

(I)求证:

(II)若

正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
17.对于给定数列



(Ⅰ)已知数列{bn}是“M类数列”且bn=2n,求它对应的实常数p,q的值;
(Ⅱ)若数列{cn}满足c1=1,cn+1-cn=2n(n∈N*),求数列{cn}的通项公式.并判断{cn}是否为“M类数列”,说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!