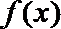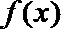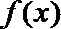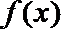- 真题试卷
- 模拟试卷
- 预测试卷
1.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数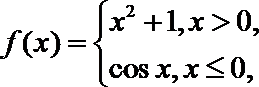
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数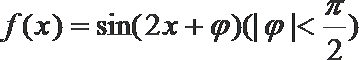
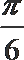
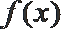
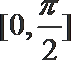
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图是函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设命题






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当

当

(2)①当




当




②当
当且仅当

综合①、②知

所以为9千件时,该企业生产此产品获利最大.
解析
解析已在路上飞奔,马上就到!
知识点
18.在







(1)求证:
(2)设圆






正确答案
(1)证明:由正弦定理得

即sin2A=sin2B ∴2A=2B或2A+2B=π,
即A=B或A+B=∵
由A+B=可知c=,∴ΔABC是直角三角形
(2)由(1)及

在RtΔ

所以,




当


解析
解析已在路上飞奔,马上就到!
知识点
19.在



(1)求
(2)求
正确答案
(1)

即:

又在




(2)





解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数






(1)求

(2)证明:当

正确答案
解:方法一:(1)由

又

所以

令




当


所以当

且极小值为

(2)证明:令

由(1)得,
故




解析
解析已在路上飞奔,马上就到!
知识点
22.已知二次函数





(1)若曲线




(2)

正确答案
(1)依题可设


又





设

当且仅当


当


当

(2)


当




当


若













函数

综上,当


当



函数

当


解析
解析已在路上飞奔,马上就到!